本文导论
2021秋的深度学习课程结课,本文做一个回顾。由于课程内容为CS231n 2021,因此本文相当于回顾CS231n。文章比预想写得长了很多,但没有多少个人的内容,权当复述了。
深度学习是机器学习的一种,现在广泛应用于人工智能的任务中。在这些任务里,传统学习算法对高维的数据泛化能力不足,其中实现泛化的机制不适合学习高维空间中复杂的函数。这方面的论述现在已经非常地多。深度学习则旨在克服这种困难、解决其它传统算法难以解决的问题。
一种解释深度学习的角度是,学习数据的表示。应用简单的机器学习算法时,一般先从数据提取一个合适的特征集,然后将这些特征传入模型。但显然一般是很难知道什么样的特征对当前任务是有效的,解决这个问题的方案之一就是用机器学习来发掘表示本身,即“表示学习”。这种方案就没有了人工设计表示所需要的大量时间和精力这样的缺陷。深度学习则将复杂的表示用一系列简单的表示来表达。简单的特征经过逐层处理,特征逐步抽象,最终得到我们需要的高级复杂特征。
数据、模型和算力的发展让机器学习特别是深度学习能够大放异彩。当下时代,数据量与日俱增,而深度模型都有着较为强大的拟合能力,于是越庞大的数据就让深度模型的表现越为优异,甚至能够在某些困难任务上超过人类的表现。(进来也有非常多的对如何降低数据量要求的研究,例如试图通过无监督或半监督学习充分利用大量的无标签样本。)而当下更新换代十分迅速的用于深度学习训练的硬件,CPU、GPU等,也让训练变得越来越快,这就和模型规模的增加相互适配,不至于让训练时间也迅速上涨。
由于CS231n主要面向CV(计算机视觉),下面的内容也围之展开。
Contents
- 1 本文导论
- 2 Lecture 3,4 : Loss Functions and Optimization; Neural Networks and Backpropagation
- 3 Lecture 5: Convolutional Neural Networks
- 4 Lecture 6: Deep Learning Hardware and Software
- 5 Lecture 7,8 : Training Neural Networks
- 6 Lecture 9: CNN Architectures
- 7 Lecture 10: Recurrent Neural Networks
- 8 Lecture 11: Attention and Transformers
- 9 Lecture 12: Generative Modeling
- 10 Lecture 13: Self-supervised Learning
- 11 Lecture 14,15 : Visualizing and Understanding, Detection and Segmentation
Lecture 3,4 : Loss Functions and Optimization; Neural Networks and Backpropagation
Neural Network
很多神经网络首先将\boldsymbol{x}通过一次线性变换、然后将得到的值传入一个被称为激活函数的函数里,这里的变换参数由学习得到,而激活函数则事先给定。通过激活函数,这个变换变成了非线性的。这种类型的非线性变换当然可以复合起来,这些函数复合连接在一个链上就形成了一个\phi,从而模型可取为作用于\phi(\boldsymbol{x})的线性模型。这些链式结构是神经网络中最常用的结构。
Loss function
如果说目标是从数据\{(\boldsymbol x_i,y_i)\}里学习,从而用函数f(\boldsymbol{x};\boldsymbol{\theta})近似目标函数f^*,那么要做的就是学习参数\boldsymbol{\theta}的值,使它能够得到最佳的函数近似。损失函数就用来看模型的拟合优劣,一个好的模型,当然应试图使所有数据上的损失尽可能小。不过,往往只能够在训练集上做到这一点。课程里提到了两种经典的loss:用于SVM的hinge loss以及用于softmax的cross entropy loss。
Optimization
确定损失函数后,就变成一个优化问题:在函数类里找到一个最小化训练集总代价的函数,也就是找到相应的模型参数。这个优化问题当然是非凸的。一种简单易行的做法是梯度下降。将模型的全参数记为\boldsymbol{w},首先为其取一个初值,然后计算\nabla_\boldsymbol{w}L,然后更新参数:\boldsymbol{w}\leftarrow \boldsymbol{w}-\eta\, \nabla_\boldsymbol{w}L,这里\eta称为学习率。重复这一更新过程,那么\boldsymbol{w}就有望收敛于我们需要的参数值,所以我们重复更新过程直至\nabla_\boldsymbol{w}L足够小,这时更新已经非常小,或已达到了收敛。如果看凸优化,梯度下降则保证达到全局最小,但在这里则并非如此——这里的优化问题是非凸的。不同的初值可能会达到不同的极小点,从而给出不一样的结果。由于梯度的计算需要计算数据集大小的数量的平均,为了减轻计算负担,一般用一个mini-batch的样本的平均来近似代替。
Backpropagation
计算梯度的一种流行策略是BP算法。构建计算图后,基于多元微分学里的链式法则,计算出梯度的数值。
Lecture 5: Convolutional Neural Networks
介绍CNN。“卷积神经网络’’ 一词表明该网络使用了卷积这种数学运算,是一种特殊的线性运算。将一般的卷积离散化,并将核kernel相对输入进行翻转flip,就得到了CNN中使用的卷积运算。具有很好的性质。
CNN中的典型层还有池化(pooling)层、经典的全连接(Fully connected)层。
CNN是广泛应用于CV的经典神经网络。
Lecture 6: Deep Learning Hardware and Software
Hardware
CPU
GPU
Software
Pytorch
TensorFlow
本人主要学习Pytorch。
torch.Tensor
torch.autograd
torch.nn
torch.optim
PyTorch的三个抽象的层级:barebone、nn.Module、nn.Sequential,比较如下:
| API | Flexibility | Convenience |
|---|---|---|
| Barebone | High | Low |
nn.Module |
High | Medium |
nn.Sequential |
Low | High |
Lecture 7,8 : Training Neural Networks
Activation Functions
一般认为Sigmoid和tanh不是好的选择——容易饱和、exp()不便计算、Sigmoid输出非零中心。
在现代神经网络中,默认的推荐是由激活函数\max\{0,z\}定义的整流线性单元,或称为ReLu。ReLu和上面两个函数相比,计算高效、收敛更快。
ReLu的一个缺陷是它们不能通过基于梯度的方法学习那些使它们激活为零的样本。ReLu的各种扩展保证了它们能在各个位置都接收到梯度。这些拓展大多数的表现比得上ReLu,并且偶尔表现得更好。
有三个基于ReLU的拓展,它们当z_i<0时使用一个非零的斜率\alpha_i:h_i=g(\boldsymbol{z},\boldsymbol{\alpha})_i=\max(0,z_i)+\alpha_i\min(0,z_i)。
- 绝对值整流固定\alpha_i=-1来得到g(z) = |z|。
- 渗漏整流线性单元(Leaky ReLU)将\alpha_i固定成一个类似 0.01 的小值。
- 参数化整流线性单元(parametric ReLU)或者PReLU 将\alpha_i作为学习的参数。
此外还有,
- Exponential Linear Units (ELU):具有ReLu的优点,且还具有近似零均值输出、Negative saturation regime compared with Leaky ReLU adds some robustness to noise。表达式为:\max(0,z_i)+\alpha(\exp(\min(0,z_i))-1),其中\alpha默认为1。
- Scaled Exponential Linear Units (SELU):表达式为\lambda\cdot\operatorname{ELU}(z_i),具有 Self-normalizing 的性质、可以不用搭配BatchNorm训练网络。
- maxout单元则进一步扩展了整流线性单元。maxout单元将z划分为每组具有k个值的组,而不是使用作用于每个元素的函数g(z)。每个maxout单元则输出每组中的最大元素,这提供了一种方法来学习对输入\boldsymbol{x}空间中多个方向响应的分段线性函数。
- Swish:z\, \sigma(\beta z)
Data Preprocessing
数据中心化、PCA、Whitening。对图像来说,后二者不常见。中心化可以有:减去每个像素对应位置的均值(Subtract the mean image)、减去每个channel的所有图所有位置的均值(Subtract per-channel mean, 3 numbers)、减去每个channel的均值和标准差。
Weight Initialization
随机小数字初始化(深层网络不适用)
“Xavier” Initialization: \mathrm{rand}/\sqrt{d_{\mathrm{in}}}。 (Xavier假设了零中心化的激活函数。)
Kaiming / MSRA Initialization: \sqrt{2/d_{\mathrm{in}}}\cdot\mathrm{rand}。(ReLu)
Batch Normalization
BN一般在FC层/卷积层后,激活函数前。能使深度网络更容易训练,让梯度更好地flow,可以使用更高的学习率、得到更快的收敛,对权重初始化更稳健,训练时起到regularization的作用。
如果输入是维度(B,L),要学习的是L维向量\boldsymbol{\gamma},\boldsymbol{\beta};首先对L维每个维度减去batch的均值以及标准差,\mu_j=\frac1B\sum_{i=1}^B x_{ij}, \sigma_j^2=\frac1B\sum_{i=1}^B(x_{ij}-\mu_j)^2, \hat x_{ij}=\frac{x_{ij}-\mu_j}{\sqrt{\sigma_j^2+\varepsilon}},然后输出是y_{ij}=\gamma_j\hat x_{ij}+\beta_j;测试时则使用训练的\boldsymbol\mu,\boldsymbol\sigma^2的均值估计。
类似地,如果输入维度(B,C,L),那么上述向量都是C维向量。
对于图像类型的输入,维度(B,C,H,W),那么上述向量也都是C维向量。
此外,还有Layer Normalization的操作。这种操作在训练和测试是一样的,可用于RNN。对(B,L)的输入,均值和标准差是在L维里进行而非在B的batch进行,而\boldsymbol{\gamma},\boldsymbol{\beta}仍是L维向量。对(B,C,H,W)的输入,均值和标准差是B维向量。
此外,还有Instance Normalization。也是训练测试一样的操作。这里\mu和\sigma^2变为了矩阵(B,C),即每个样本的每个channel用自己的均值和标准差来normalize。
Transfer learning
实际训练中,人们很少从头训练CNN,因为拥有的数据集的数量和“充分”比较还是有所欠缺。因而常见的做法是,在一个非常大的数据集上pretrain一个卷积网络,然后使用这个预训练模型来作为初始化,或者利用它来做特征提取器。以下是常见场景:
- 固定的特征提取器。移去预训练模型最后一层,用预训练模型做特征提取。
- Fine-tuning。在预训练模型的基础上继续BP。这其中,既可以fine-tune所有层的参数,也可以只fine-tune后面的层的参数。这种做法基于的考虑是早期特征是更为一般的,就是说适用于更多数的任务,但是后面层的特征就已经高度复杂化、特殊化(于原数据集)。
(Fancier) Optimizers
momentum
梯度下降有时过程会很慢,有时会受困于局部极值。动量法旨在加速学习,并有一定希望脱离局部极值。动量算法积累了之前梯度指数级衰减的移动平均,并且继续沿该方向移动。从形式上看,动量算法引入了变量v充当速度角色——它代表参数在参数空间移动的方向和速率。速度被设为负梯度的指数衰减平均。名称动量(momentum)来自物理类比,根据牛顿运动定律,负梯度是移动参数空间中粒子的力。动量在物理学上定义为质量乘以速度。在动量学习算法中,我们假设是单位质量,因此速度向量v也可以看作是粒子的动量。超参数\alpha\in[0,1)决定了之前梯度的贡献衰减得有多快。更新规则为:\boldsymbol{v}\leftarrow\alpha\boldsymbol v-\epsilon \boldsymbol g,\, \boldsymbol \theta\leftarrow\boldsymbol \theta+\boldsymbol v。相对于\epsilon,\alpha越大,之前梯度对现在方向的影响也越大。
现在,步长取决于梯度序列的大小和排列。当许多连续的梯度指向相同的方向时,步长最大。如果动量算法总是观测到梯度\boldsymbol{g},那么它会在方向-\boldsymbol g上不停加速,直到达到最终速度,其中步长大小为\epsilon|\boldsymbol g|/(1-\alpha),因此将动量算法的超参数视为1/(1-\alpha)有助于理解。例如,\alpha=0.9对应着最大速度10倍于普通算法。
在实践中,\alpha的一般取值为0.5, 0.9, 0.99。和学习率一样,\alpha也会随着时间不断调整。一般初始值是一个较小的值,随后会慢慢变大。随着时间推移调整\alpha没有收缩\epsilon重要。
Nesterov Momentum则将梯度由当前点的梯度改为了经过\boldsymbol v后的点的梯度。即:原算法是\boldsymbol{v} _ {t+1}=\alpha\boldsymbol v _ t-\epsilon \boldsymbol g(\boldsymbol\theta _ t),改为了\boldsymbol{v} _ {t+1}=\alpha\boldsymbol v _ t-\epsilon \boldsymbol g(\boldsymbol\theta _ {t}+\alpha\boldsymbol v _ t)。(如果进行换元\tilde{\boldsymbol\theta} _ t={\boldsymbol\theta} _ t+\alpha\boldsymbol v _ t后变为:\boldsymbol{v} _ {t+1}=\alpha\boldsymbol v _ t-\epsilon \boldsymbol g(\tilde{\boldsymbol\theta} _ {t}), \tilde{\boldsymbol\theta} _ {t+1}={\boldsymbol\theta} _ t+\boldsymbol v _ {t+1}+\epsilon(\boldsymbol v _ {t+1}-\boldsymbol v _ t)。)Nesterov动量可以解释为往标准动量方法中添加了一个校正因子。在凸批量梯度的情况下,Nesterov动量对额外误差收敛率有所改进,可惜在随机梯度的情况下,Nesterov动量没有改进收敛率。
AdaGrad
AdaGrad算法,独立地适应所有模型参数的学习率,缩放每个参数反比于其所有梯度历史平方值总和的平方根。具有损失最大偏导的参数相应地有一个快速下降的学习率,而具有小偏导的参数在学习率上有相对较小的下降。
计算累计平方梯度\boldsymbol r\leftarrow\boldsymbol r+\boldsymbol g\odot\boldsymbol g,然后计算更新(记全局学习率\epsilon,小常数\delta为数值稳定大约设10^{-7})\boldsymbol\theta\leftarrow\boldsymbol\theta\boldsymbol-\frac{\epsilon}{\sqrt r+\delta}\boldsymbol g。
在凸优化背景中,AdaGrad算法具有一些好的理论性质。然而,经验上已经发现,对于训练深度神经网络模型而言,从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。AdaGrad在某些深度学习模型上效果不错,但并非全部。
RMSProp
RMSProp算法修改AdaGrad以在非凸设定下效果更好,改变梯度积累为指数加权的移动平均。AdaGrad旨在应用于凸问题时快速收敛。当应用于非凸函数训练神经网络时,学习轨迹可能穿过了很多不同的结构,最终到达一个局部是凸碗的区域。AdaGrad根据平方梯度的整个历史收缩学习率,可能使得学习率在达到这样的凸结构前就变得太小了。RMSProp使用指数衰减平均以丢弃遥远过去的历史,使其能够在找到凸碗状结构后快速收敛,它就像一个初始化于该碗状结构的AdaGrad算法实例。经验上,RMSProp已被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习经常采用的优化方法之一。
累积变量每轮更新为\boldsymbol{r}\leftarrow\rho\boldsymbol r+(1-\rho)\, \boldsymbol g\odot\boldsymbol g,参数更新为\boldsymbol\theta\leftarrow\boldsymbol \theta-\frac{\epsilon}{\sqrt{\boldsymbol r}+\delta}\boldsymbol g。
Adam
Adam是另一种学习率自适应的优化算法。“Adam’’ 这个名字派生自短语“adaptive moments’’。
首先,在Adam 中,动量直接并入了梯度一阶矩(指数加权)的估计。将动量加入RMSProp最直观的方法是将动量应用于缩放后的梯度。结合缩放的动量使用没有明确的理论动机。其次,Adam 包括偏置修正,修正从原点初始化的一阶矩(动量项)和(非中心的)二阶矩的估计。RMSProp 也采用了(非中心的)二阶矩估计,然而缺失了修正因子。因此,不像Adam,RMSProp二阶矩估计可能在训练初期有很高的偏置。Adam通常被认为对超参数的选择相当稳健,尽管学习率有时需要从建议的默认修改。
Adam算法:给定\eta(建议默认为0.001)、矩估计的指数衰减速率\rho_1,\rho_2\in[0,1)(建议默认为0.9、0.999)、用于数值稳定的小常数\delta(建议默认为10^{-8})、初始参数\boldsymbol{\theta},初始化一阶和二阶矩变量\boldsymbol s=0,\, \boldsymbol r=0,时间步t=0,计算梯度\boldsymbol g后令t\leftarrow t+1,
\begin{aligned}\text{更新有偏一阶矩估计:}&\boldsymbol{s}\leftarrow \rho_1\boldsymbol s+(1-\rho_1)\boldsymbol{g}\\ \text{更新有偏二阶矩估计:}&\boldsymbol r\leftarrow\rho_2\boldsymbol r+(1-\rho_2)\boldsymbol{g}\odot\boldsymbol{g}\\ \text{修正一阶矩的偏差:}&\boldsymbol{\hat{s}}\leftarrow\frac{\boldsymbol s}{1-\rho_1^t}\\ \text{修正二阶矩的偏差:}&\boldsymbol{\hat{r}}\leftarrow\frac{\boldsymbol r}{1-\rho_2^t}\\ \text{计算更新:}&\Delta\boldsymbol\theta=-\eta\frac{\boldsymbol{\hat s}}{\sqrt{\boldsymbol{\hat s}+\delta}}\quad\text{(逐元素操作)}\\ \text{应用更新:}&\boldsymbol \theta\leftarrow\boldsymbol\theta+\Delta\boldsymbol\theta\end{aligned}
算法中t的上标是指幂次。
二阶优化算法
牛顿法
牛顿参数更新规则:\boldsymbol{\theta}^{*}=\boldsymbol{\theta}_{0}-{H}^{-1} \nabla_{\boldsymbol{\theta}} J\left(\boldsymbol{\theta}_{0}\right)。只要Hessian 矩阵保持正定,牛顿法能够迭代地应用。在深度学习中,目标函数的表面通常非凸,如鞍点。因此使用牛顿法是有问题的。如果Hessian矩阵的特征值并不都是正的,例如,靠近鞍点处,牛顿法实际上会导致更新朝错误的方向移动。
牛顿法用于训练大型神经网络还受限于其显著的计算负担。Hessian矩阵中元素数目是参数数量的平方,因此,如果参数数目为k(甚至是在非常小的神经网络中k也可能是百万级别),牛顿法需要计算k\times k矩阵的逆,计算复杂度为O(k^3)。另外,由于参数将每次更新都会改变,每次训练迭代都需要计算Hessian矩阵的逆。其结果是,只有参数很少的网络才能在实际中用牛顿法训练。
拟牛顿法
Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法具有牛顿法的一些优点,但没有牛顿法的计算负担(每次O(k^2))。拟牛顿法所采用的方法(BFGS是其中最突出的)是使用矩阵M_t近似逆,迭代地低秩更新精度以更好地近似H^{-1}。
BFGS近似的说明和推导出现在很多关于优化的教科书中,这里略。
L-BFGS通过避免存储完整的Hessian 逆近似M,BFGS算法的存储代价可以显著降低。L-BFGS算法使用和BFGS算法相同的方法计算M的近似,但起始假设是M^{(t-1)} 是单位矩阵,而不是一步一步都要存储近似。CS231n课件评价为:Usually works very well in full batch, deterministic mode; Does not transfer very well to mini-batch setting.
Learning rate schedule
一个简单而又最为流行的办法是,每过若干epoch就减小学习率的值。例如:
- 按1/\sqrt t的速率衰减:\epsilon^t=\epsilon/\sqrt{t}。
- 阶梯衰减:ResNets在30、60、90epoch时学习率减小到0.1倍。
- 余弦衰减:\epsilon_t=\frac{\epsilon_0}{2}(1+\cos\frac{t\pi}{T})。
- 线性衰减:\epsilon_t={\epsilon_0}(1-\frac{t}{T})。
Linear Warmup: 初始学习率过高可能会使loss爆炸,故前面大约5000个iterations可以让学习率从0线性增长,以避免这种现象。
经验法则:如果增大batch size为N倍,学习率也变N倍。
实际中,Adam是很好的默认选择,即使学习率无schedule也效果不错。带动量的SGD可以优于Adam,但需要对学习率和schedule更多的调参(可尝试cos衰减,较少超参数)。如果可以做full batch,可以用L-BFGS。
Early stopping
在验证集表现有所下降时或训练过长时间时,停止训练。
Model Ensembles
这里指训练几个独立的模型,对测试结果求平均。
(还可以用同一个模型的不同时刻的参数)
(Polyak averaging: 使用参数的滑动平均moving average)
Regularization
Add term to loss
损失函数加上\lambda R(\boldsymbol w),其中R可取L2、L1、Elastic net的正则化等。
Dropout
计算开销不大,但是十分强大的正则化方法,可被认为是集成大量深层神经网络的实用Bagging方法。Bagging学习,是定义k个不同的模型,从训练集有放回采样构造k个不同的数据集,然后在训练集i上训练模型i。Dropout的目标是在指数级数量的神经网络上近似这个过程。
Dropout训练的集成包括所有从基础网络除去非输入输出单元后形成的子网络,只需将一些单元的输出乘零就能有效地删除一个单元。推断时,Dropout对指数多个模型进行平均,但这是难以计算的。一种近似方法是,权重比例推断规则(weight scaling inference rule),目前还没有在深度非线性网络上对这种近似推断规则的准确性作任何理论分析,但经验上表现得很好。做法是:该模型具有所有单元,但我们将单元的输出的权重乘以该单元的被包含概率。这个修改的动机是得到从该单元输出的正确期望值。
Data Augmentation
如,翻转,随机裁剪、放缩,Color Jitter如对比度和亮度,平移旋转拉伸……
DropConnect
权重置0
Fractional Pooling
训练时使用随机的池化区域,测试时平均预测。
Stochastic Depth
训练时随机跳过一些层,测试时使用所有层。
Cutout
训练时置图片随机区域为0,测试时使用全部图片。
Mixup
在随机混合的图片上训练,在原图片测试。
实际应用中
大的全连接层,考虑dropout;Batch normalization和data augmentation总是好的做法;对小的分类数据集尝试用cutout和mixup
Choosing Hyperparameters
- 察看初始损失。关闭weight decay,检查初始loss是否异常,如对C类的softmax应约为\ln C。
- 在小样本上过拟合。尝试在小样本(约5到10mini-batches)100%的训练准确度;调节网络架构、学习率、权重初始化。(loss不下降?——>学习率低,或初始化差;loss变成Inf或NaN?——>学习率高,或初始化差)
- 寻找使得loss下降的学习率。用上一步的架构,使用所有的训练数据,打开小的weight decay,找到在大约100iterations内使loss显著下降的学习率。(推荐尝试学习率:1e-1、1e-2、1e-3、1e-4)
- 在上一步周围选择一些学习率和weight decay,训练1-5eopchs。(推荐尝试weight decay:1e-4、1e-5、0)
- 训练更长时间(10-20epochs)而不开学习率衰减。
- 观察loss曲线。如果train和val都上升,说明还要继续训练;二者gap巨大,说明过拟合,应增加正则化、获取更多数据;二者gap非常小,说明欠拟合,应训练更长时间,或使用更大的模型。
Lecture 9: CNN Architectures
介绍一些著名的CNN架构:AlexNet、ZFNet、VGG、GoogleNet、ResNet、SENet、Wide ResNet、ResNeXT、DenseNet、MobileNets、NASNet、EfficientNet等。
AlexNet
2012
Architecture: CONV1->MAX POOL1->NORM1->CONV2->MAX POOL2->NORM2->CONV3->CONV4->CONV5->Max POOL->FC6->FC7->FC8
清楚结构的可见:link
AlexNet:首先使用了ReLu、使用了normalization、大量的数据增强、dropout(0.5)、带动量SGD(0.9)、学习率在验证集准确率平缓后减到1/10,L2正则化(5e-4)
ZFNet
2013
在AlexNet上改进了超参
VGGNet
2014
更小的filter,更深的网络:从AlexNet的8层变为16-19层,只有3×3的stride1、pad1的CONV核及2×2的stride2的max pool核。(例如3个3×3的stride1的卷积层和一个7×7等等卷积层有相同的effective receptive field,但是更深,有更多的非线性,以及更少的参数:3\times(3^2C^2) vs 7^2C^2 其中C为每层channel数)
VGG16结构可见:link

GoogleNet
2014
更深的网络(22层),但更高的计算效率。
VGG16共138M参数,GoogleNet只有5M参数。使用“Inception”模块,中间无FC层。
“Inception module”: design a good local network topology (network within a network) and then stack these modules on top of each other.
网络结构可见:link

ResNet
2015
非常深的使用残差连接residual connections的网络。
motivation: 更深的网络有更强的表示能力(更多的参数),因而更深的模型不如浅模型的原因可能是深模型更难优化。如果要让深模型至少表现得像浅模型一样好,一个方案是在浅层模型的基础上加上恒等映射层。于是尝试用网络的隐层拟合残差映射,而非直接拟合所需目标函数。
Every residual block has two 3x3 conv layers; Periodically, double # of filters and downsample spatially using stride 2 (/2 in each dimension)
原始配置:每一CONV后都接BatchNorm;带动量SGD(0.9);学习率在验证集准确率平缓后减到1/10;weight decay 1e-5;无dropout
比较

An Analysis of Deep Neural Network Models for Practical Applications, 2017.
VGG:最多的参数、最多的运算;GoogleNet:最高效;AlexNet:计算量小但内存开销大、准确率低;ResNet:不错的效率(取决于层数),高准确率
SENet
2017
Add a “feature recalibration” module that learns to adaptively reweight feature maps
Global information (global avg. pooling layer) + 2 FC layers used to determine feature map weights
Wide ResNet
2016
Argues that residuals are the important factor, not depth
User wider residual blocks (F x k filters instead of F filters in each layer)
50-layer wide ResNet outperforms 152-layer original ResNet
Increasing width instead of depth more computationally efficient (parallelizable)
ResNeXT
2016
DenseNet
2017
Showed that shallow 50-layer network can outperform deeper 152 layer ResNet.

MobileNets
2017
大大提升效率,但只有很少的准确率损失。
NASNet
Use NAS to find best cell structure on smaller CIFAR-10 dataset, then transfer architecture to ImageNet
Neural Architecture Search with Reinforcement Learning (NAS) 2016
EfficientNet
Increase network capacity by scaling width, depth, and resolution, while balancing accuracy and efficiency.
Search for optimal set of compound scaling factors given a compute budget (target memory & flops).
Scale up using smart heuristic rules.
比较
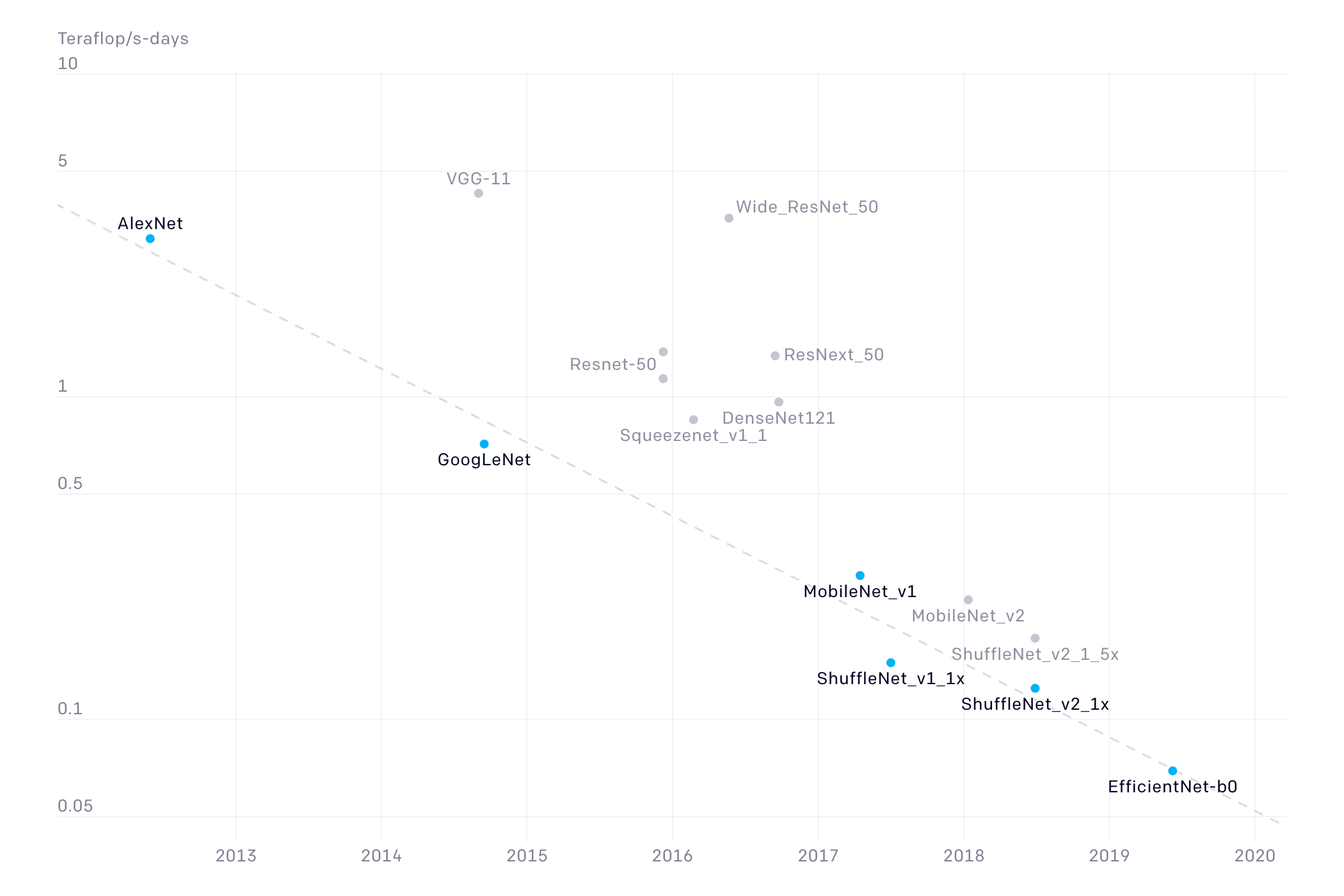
概括
AlexNet说明了CNN对CV的可行性;VGG说明更深的网络表现更好;GoogleNet关注efficiency,使用1×1卷积和global avg pool代替FC层;ResNet提供了训练超深网络的方法;这之后,关注转移到了高效的网络上,旨在能在移动设备使用,如MobileNet、ShuffleNet;而NAS可用于网络结构的自动设计。
实际中,ResNet和SENet是很好的默认选择。
Lecture 10: Recurrent Neural Networks
循环神经网络(recurrent neural network)或RNN是一类用于处理序列数据的神经网络。就像卷积网络是专门用于处理网格化数据(如一个图像)的神经网络,循环神经网络是专门用于处理序列\boldsymbol x^{(1)},\dots,\boldsymbol x^{(\tau)}的神经网络。
RNN的内容,由于打算在CS224n再作回顾,这里不写太多。
Vanilla RNN: \boldsymbol h_t=\tanh(W_{hh}\boldsymbol h_{t-1}+W_{xh}\boldsymbol x_t), \boldsymbol y_t=W_{hy}\boldsymbol h_t.
Truncated Backpropagation through time: 前向和反向在一块一块的子序列上进行,而非全部序列。
LSTM、GRU
Lecture 11: Attention and Transformers
Attention和Transformer的内容,由于打算在CS224n再作回顾,这里不写太多。
以Image Captioning为例,attention的使用其实和NLP中的几乎无异。Encoder侧,在图片\boldsymbol I经过CNN得到特征(假设维度为三维D\times H\times W),将其经过变换得到\boldsymbol h_0。Decoder侧,每次输出为\boldsymbol y_t=g(\boldsymbol y_{t-1},\boldsymbol h_{t-1},\boldsymbol c),其中\boldsymbol c为context vector,可取为\boldsymbol c=\boldsymbol h_0。这里\boldsymbol c成为了信息瓶颈,为解决这个问题,考虑attention这一方案:每步的context vector会attend图像的不同区域。Decoder变为\boldsymbol y_t=g(\boldsymbol y_{t-1},\boldsymbol h_{t-1},\boldsymbol c_t),context vector计算如下:先计算attention score,对t\in{1,\dots, D},Z_t为第t维H\times W特征,E_{t}=f_{\mathrm{att}}(\boldsymbol h_{t-1},Z_t)\in\mathbb R^{H\times W},然后计算attention分布,A_t=\mathrm{softmax}(E_t)\in\mathbb R^{H\times W};得到context向量\boldsymbol c_t\in\mathbb R^D,其中c _ t=\sum _ {i,j}(A _ t) _ {i,j}(Z _ t) _ {i,j}。利用此\boldsymbol c _ t即可计算输出\boldsymbol y _ t=g(\boldsymbol y _ {t-1},\boldsymbol h _ {t-1},\boldsymbol c _ t)。
Lecture 12: Generative Modeling
Generative Modeling:设数据生成发布为p_{\mathrm{data}},在训练数据的基础上,通过学习,得到其近似分布p_{\mathrm{model}},再从这个分布里抽样。
这个过程中,有些模型允许显式地计算概率分布函数,有些则不允许,只能支持隐式获取分布知识的操作,如从分布中采样。在CS231n中,前者介绍有PixelRNN/PixelCNN、变分自编码器Variational Autoencoder (VAE),后者介绍了生成式对抗网络Generative Adversarial Network (GAN)。
PixelRNN, PixelCNN
利用公式p(\boldsymbol x)=\prod p(x_i\mid x_1,\dots,x_{i-1})来计算,然后最大化训练集的似然即可。由于条件分布也很复杂,考虑使用神经网络来表达。
PixelRNN使用RNN(如LSTM)表达条件分布,生成时从图像的一个角开始生成新图片。这样做的缺陷显然是RNN带来的序列生成的低速,无论是训练还是推断。
PixelCNN的训练则较之快很多,但生成依然很慢(对32×32的图片,网络需要做前向1024次)。条件分布换为了masked CNN(对当前像素点,filter的context region以它为中心,mask掉在这个点“未来”的点,再进行之后的CNN)
不是很了解。
Variational Autoencoders (VAE)
VAE可以一次性生成所有pixel,使用的是公式p_{\boldsymbol\theta}(\boldsymbol x)=\int p_{\boldsymbol\theta}(\boldsymbol z)p_{\boldsymbol\theta}(\boldsymbol x| \boldsymbol z)\, \mathrm{d}\boldsymbol z,其中\boldsymbol z是隐变量。这种做法无法直接优化,VAE做的是,推导似然的下界然后优化。
先来回顾autoencoder,即“自编码器”,经过训练后能尝试将输入复制到输出,包含encoder和decoder。当然,如果一个autoencoder只是简单地学会将处处设置为Dec(Enc(x))=x,那么这个autoencoder就没有什么用处。我们并不应将其设计成输入到输出完全相等,这通常需要向autoencoder强加一些约束,使它只能近似地复制,并只能复制与训练数据相似的输入。这些约束强制模型考虑输入数据的哪些部分需要被优先复制,因此它往往能学习到数据的有用特性。
于是,若输入\boldsymbol x经过encoder得到\boldsymbol z,可以认为\boldsymbol z就是原数据的一组特征;由于这个特征的维度要比原输入小(提取有用的特性),因而也可以用于降维 (dimensionality reduction) 这一过程。如果这个autoencoder足够好,那么\boldsymbol z就可以用于监督学习里面了。(这也有了从大量的未标注数据集迁移到少量的带标注数据集的效果。)
如果\boldsymbol z经过decoder,得到的输出和原输入足够接近,那么就可以认为这是比较好的。
将\boldsymbol z视为隐变量,可得这里的生成式建模:variational autoencoder。考虑decoder侧,新数据是在生成\boldsymbol z后得到的分布中采样生成,\boldsymbol z的先验分布可取为简单的分布,如正态分布,用于decoder的数据生成的后验分布p_{\boldsymbol \theta}(\boldsymbol x|\boldsymbol z)是复杂分布,可以用神经网络表示。常见地,数据的似然函数可以作如下分解:
\ln p(\boldsymbol x)=\mathcal L(q)+D_{\mathrm{KL}}(q\|p)
其中
\begin{gathered}
\mathcal L(q)=\int q(\boldsymbol z)\ln\frac{p(\boldsymbol x,\boldsymbol z)}{q(\boldsymbol z)}\, \mathrm d\boldsymbol z=\mathbb E_{\mathbf z\sim q}[\ln p(\boldsymbol x, \mathbf z)]+H(q),\\
D_{\mathrm{KL}}(q\|p)=-\int q(\boldsymbol z)\ln\frac{p(\boldsymbol z|\boldsymbol x)}{q(\boldsymbol z)}\,\mathrm d\boldsymbol z\geqslant0.
\end{gathered}
由于优化\ln p(\boldsymbol x)较难,所以我们考虑优化其证据下界ELBO \mathcal L(q),将其写成
\mathcal L(q)=\mathbb E_{\mathbf z\sim q}[\ln p(\boldsymbol x| \mathbf z)]-D_{\mathrm{KL}}(q(\boldsymbol z)\|p(\boldsymbol z)).
现在对q(\boldsymbol z)的范围作一定限制,这个限制体现在encoder上,即\boldsymbol z是由原数据\boldsymbol x encode而来,那么q(\boldsymbol z)应是给定\boldsymbol x后得到的条件分布,这个条件分布的参数就是encoder的参数了。这个条件分布我们取正态分布。
现在上式第一项是关于decoder的,最大化它体现了decoder要尽可能还原\boldsymbol x;第二项是关于encoder的,体现了encoder应尽可能让条件分布q(\boldsymbol z)尽量接近所选的正态先验p(\boldsymbol z)=\mathcal N(\boldsymbol z;\boldsymbol 0,I)。两项均是可以处理的,第一项实践中常常采样\boldsymbol z\sim q来粗略近似,第二项是两个正态分布间的KL散度,是有显式表达式的,可见wikipedia。于是,网络的前向过程就可描述为:输入\boldsymbol x经过encoder,得到参数\boldsymbol \mu_{\mathrm e},\boldsymbol \sigma^2_{\mathrm e},从而得到\boldsymbol z=\boldsymbol \mu_{\mathrm e}+\epsilon\boldsymbol \sigma^2_{\mathrm e}(其中\epsilon\sim N(\boldsymbol 0,I)),这个\boldsymbol z经过decoder,得到参数\boldsymbol \mu_{\mathrm d},\Sigma_{\mathrm d},进而得到\hat{\boldsymbol x},\mathcal L。然后只需要对\mathcal L反向传播进行优化就可以了。
训练得到encoder和decoder的参数后,就可以利用它们生成新数据了。从先验p(\boldsymbol z)=\mathcal N(\boldsymbol 0;I)中采样,然后传入decoder得到参数,再用这参数就可以采样得到新样本了。这种生成易于实现,速度较快,也获得了出色的结果,是生成式建模中的最先进方法之一。它的主要缺点是从在图像上训练的变分自编码器中采样的样本往往有些模糊。这种现象的原因尚不清楚。
Generative Adversarial Networks (GANs)
GAN不显式地建模概率密度。只需要从简单分布抽样,如random noise,然后学习到训练分布的变换。
生成式对抗网络基于博弈论场景,其中生成器网络必须与对手竞争。生成器网络(Generator network)直接产生样本\boldsymbol x=g(\boldsymbol z);其对手, 判别器网络(discriminator network),试图区分从训练数据抽取的样本和从生成器抽取的样本。判别器d(\boldsymbol x)给出的概率值,指示生成的样本是真实训练样本而不是从模型抽取的伪造样本的概率。
形式化表示GAN中学习的最简单方式是零和游戏, 其中函数v(\boldsymbol\theta^{(g)},\boldsymbol\theta^{(d)})确定判别器的收益,生成器接收-v(\boldsymbol\theta^{(g)},\boldsymbol\theta^{(d)})作为它自己的收益。在学习期间,两边尝试最大化自己的收益,因此收敛在
g^\ast=\operatorname*{\arg\min}_g\max_d v(g,d).
v的默认选择是
v(\boldsymbol\theta^{(g)},\boldsymbol\theta^{(d)})=\mathbb E_{\mathbf x\sim p_{\mathrm{data}}}\log d(\mathbf x)+\mathbb E_{\mathbf x\sim p_{\mathrm{model}}}\log(1-d(\mathbf x)).更具体的写法是
\mathbb E_{\mathbf x\sim p_{\mathrm{data}}}\log d(\mathbf x;\boldsymbol \theta^{(d)})+\mathbb E_{\mathbf z\sim p(\boldsymbol z)}\log(1-d(\boldsymbol g(\mathbf z;\boldsymbol \theta^{(g)});\boldsymbol \theta^{(d)})).在收敛时,生成器的样本与实际数据不可区分,并且判别器处处都输出\frac12。然后就可以丢弃判别器。
判别器达到max后,我们要将生成器达到min,这时上式左边由于和生成无关,可以忽略,然后就是优化\mathbb E_{\mathbf x\sim p_{\mathrm{model}}}\log(1-d(\mathbf x)),但实际这个优化效果不好,以下是一个可能的解释:如果作出\log(1-t)的图像可以发现,t接近0梯度小、t接近1梯度大,而这与生成器的期望相反,生成器的目标是让d(\boldsymbol x)靠近1,d(\boldsymbol x)接近0说明判别器认为这图片很可能是伪造的,这时生成器就应该需要更大的梯度让d(\boldsymbol x)往右。于是生成器的优化目标改为\max \mathbb E_{\mathbf x\sim p_{\mathrm{model}}}\log d(\mathbf x),这样对于生成不好的样本会有大得多的梯度了。这种做法得到了好得多的效果,也是当下的标准做法。
GAN的结果还有在向量上的线性性质。(如:Smiling woman - Neutral woman + Neutral man = Smiling Man)
GAN的缺点在于训练技巧性强,训练更不稳定。此外,还有生成趋同(只生成一种图片,混淆判别器的可能性更大)、生成结果扭曲变形等问题。而且由于没有建模概率函数,无法进行相关推断。
Lecture 13: Self-supervised Learning
现如今,自监督学习已是风靡盛极,可用前景大(CV、NLP等),而且也很有发展潜力。
这里只简单回顾cs231n中将自监督学习用于CV的做法。
在各种主流有监督学习任务都做到很成熟之后,数据成了最重要的瓶颈。得到大量label永远都是困难而且有高昂代价的。在大量的无标签数据中进行学习,其重要性不言而喻,如果能“半自动”地得到标签当然好极。利用数据自身来做到这点——”自“监督,很可以考虑。
Pretext tasks
pretext任务,是用来得到学习的表示的自监督任务,它们和监督学习任务一起学习,但所用的标签是自己自动生成的。CV里的pretext任务例如有图像补全、旋转角度判断、拼图、上色,等等。一般来说,这些自监督的pretext任务的表现是不被关注的,评价自监督学习得好不好,是要在下游监督学习中才能评估的。
旋转角度预测:我们的假设是:如果模型能够正确地识别一个对象的旋转角度,那么它就有了对象正常时应该如何的一种”视觉常识“。pretext任务是个四类的分类任务,将其特征提取部分迁移至下游任务即可。
相对patch位置预测:一对图像的patch,预测一个在另一个的哪个方位,pretext任务是八分类的分类任务。
图像补全:将缺失的图像经过encoder得到encoder features,这些特征经过channel-wise fully connected网络得到decoder features,decoder用它们得到补全的部分,和原图这一部分越接近,pretext任务性能就越好。其中loss用的是两个loss的和:reconstruction + adversarial learning,具体为:L=L_{\mathrm{recon}}(\boldsymbol x)+L_{\mathrm{adv}}(\boldsymbol x), L_{\mathrm{recon}}(\boldsymbol x)=|M\odot(\boldsymbol x-F_{\boldsymbol\theta}[(1-M)\odot\boldsymbol x])|^2, 而L_{\mathrm{adv}}(\boldsymbol x)=\max_D\mathbb E[\log D(\boldsymbol x)]+\log(1-D(F_{\boldsymbol\theta}[(1-M)\odot\boldsymbol x]))为真图像和补全图像的对抗损失。
图像上色:(split-brain autoencoder)idea是cross-channel predictions。channel分成两部分,各自通过不同的网络得到另一部分的预测,两个预测再拼接回来得到整体的预测。应用到监督任务时,就将两部分网络得到的特征拼接起来。
视频上色:学习不带标签的情况下,track regions or objects,因为同一物体当然得上同一种颜色。如果能建立起参考帧和输入帧的映射,那么就可以利用这个映射复制参考帧的颜色了。这个idea可以描述如下:下标i记参考帧,下标j记目标帧,建立attention map:A_{ij}=\exp(f_i^{\mathsf T}f_j)/\sum_k\exp(f_i^{\mathsf T}f_j)(f_j要attend不同的f_i),然后预测颜色y_j就等于参考颜色c_i的加权平均:y_j=\sum_i A_{ij}c_i,损失函数就是\sum_j \mathcal L(y_j,c_j)。
pretext任务关注得到一些”视觉上的常识“,但设计单独的pretext任务是很乏味的,而且得到的表示和特定的pretext任务强相关,从中得到的语义实在有限,就是说很可能不够general。这就产生了对比学习想法,这也是当下的state-of-the-art。
Contrastive Representation Learning
那么,我们期待得到的特征应该如何呢?我们希望这些特征能够表达图像和其它图像的联系程度,要对”讨厌因子“足够稳健。聚类和对比学习是两种方案,课程只介绍了对比学习,下面之对其进行回顾。
对比学习即数据有正负样本,正样本”相吸“,负样本”相斥“。一个样本通过数据增强得到的应是正样本,不同的样本间则应是负样本。当给定了一个score函数,我们的目标是学习encoder函数f,使得正对得到高的分数,负对得到低的分数,即有\mathrm{score}(f(\boldsymbol x),f(\boldsymbol x^+))>>\mathrm{score}(f(\boldsymbol x),f(\boldsymbol x^-)),其中\boldsymbol x是参考样本,\boldsymbol x^+是正样本,\boldsymbol x^-是负样本。
一个选择是InfoNCE loss:对一个正样本和其余的N-1负样本,损失函数为
\mathcal L=-\mathbb E_X\log\frac{\exp\{s(f(\boldsymbol x),f(\boldsymbol x^+))\}}{\exp\{s(f(\boldsymbol x),f(\boldsymbol x^+))\}+\sum_{j=1}^{N-1}\exp\{s(f(\boldsymbol x),f(\boldsymbol x_j^-))\}}.
注意到这和N类softmax分类的形式有一定相似。这个InfoNCE loss可以得到f(\boldsymbol x)和f(\boldsymbol x^+)的互信息量的一个下界:
\operatorname{MI}[f(\boldsymbol x), f(\boldsymbol x^+)]-\ln N\geqslant-L.
负样本数越多,即N越大,这个界越紧。
SimCLR
A Simple Framework for Contrastive Learning of Visual Representations
PIPL(PRETEXT-INVARIANT REPRESENTATION LEARNING)认为,表示应该不包含和对原图像的(pretext)变换t的信息,换言之,对t具有不变性。SimCLR也是这种想法。设变换t取自变换族\mathcal T,原输入\boldsymbol x经过不同的变换t,t',得到\tilde{\boldsymbol x}_i,\tilde{\boldsymbol x}_j,它们分别经过网络得到表示\boldsymbol h_i,\boldsymbol h_j。然后,使用一个投影网络g(\cdot)将特征投影到一个新空间,在里面进行对比学习:\boldsymbol z=g(\boldsymbol h),对\boldsymbol z_i,\boldsymbol z_j maximize agreement。
score function取余弦相似度(cosine similarity):s(\boldsymbol u,\boldsymbol v)=\boldsymbol u^{\mathsf T}\boldsymbol v/(|\boldsymbol u||\boldsymbol v|)。
完整算法:对每一样本量N的batch,对k\in\{1,\dots,N\},每次从\mathcal T取两个变换并将\boldsymbol x_k根据变换得到一对\boldsymbol z_{2k-1},\boldsymbol z_{2k},然后计算:
\begin{gathered}
\ell(i,j)=-\ln\frac{\exp(s_{i,j}/\tau)}{\sum_{k=1}^{2N}\mathbb I(k\neq i)\exp(s_{i,k}/\tau)},\\
\mathcal L=\frac1{2N}\sum_{k=1}^N[\ell(2k-1,2k)+\ell(2k,2k-1)].
\end{gathered}
优化\mathcal L来更新网络f,g。
实验表明,g(\cdot)这个投影是必要的,比在原始特征空间做对比学习效果要好,但原因尚不明确。实验表明,SimCLR需要更大的batch size(因而有必要在TPU上分布式训练)。
MoCo

Momentum Contrastive Learning
encoder和momentum encoder是相同的网络,但开始训练后参数更新不一样。负样本在动态的key队列中产生。算法描述如下:
设产生负样本的queue容量为K。对每一样本量N的batch,batch里每个样本都依次:作为query样本,经两次数据增强得到正样本\boldsymbol q,\boldsymbol k,利用q,k作为正样本对、\boldsymbol q,\boldsymbol k_i\, (i=1,\dots,K)作为负样本对计算InfoNCE损失。每个batch后,更新梯度时,更新encoder网络的参数\boldsymbol\theta_q,而momentum encoder网络的参数更新规则为\boldsymbol\theta_k\leftarrow m\boldsymbol\theta_k+(1-m)\boldsymbol\theta_q,参数更新后,queue加入现在的batch的N个\boldsymbol k,移掉里面最老的N的\boldsymbol k,这样queue一直可以有K个负样本,和batch size N“解耦”。
MoCo后来有改进版本,如结合MoCo和SimCLR的MoCo V2,这里略过了。
CPC
Contrastive Predictive Coding,属于Sequence-level的对比学习。
可用于多种学习问题,在图像的表示上不如当下的instance-level的方法有效。
粗略描述:首先将序列encode:\boldsymbol z_t=g_{\mathrm{enc}}(\boldsymbol x_t),然后在时刻t利用一个自回归(AR)模型,概括一部分序列得到context向量\boldsymbol c_t ,如果在这时要预测\boldsymbol z_{t+k},就应把当前encoder的条件下得到的\boldsymbol c_t和\boldsymbol z_{t+k}作为正样本对,其余的\boldsymbol z_{t+l}作为负样本,计算InfoNCE损失。
Other examples
CLIP (Contrastive Language–Image Pre-training) Radford et al., 2021——Contrastive learning between image and natural language sentences
Dense Object Net, Florence et al., 2018——Contrastive learning on pixel-wise feature descriptors
略。
对比学习总得来说还是比较陌生,只是知道众模型的大概做法。
Lecture 14,15 : Visualizing and Understanding, Detection and Segmentation
视情况决定是否更新。

发表回复