微积分中的一些结果

从这里开始我们将考虑一般的优化问题。首先，在微积分和线性代数里就已经可以初步接触到有很多用的性质。

定理1：若$f^{(k)}(x _ 0)=0$，其中$k=1,2,\dots,n$，且$f^{(n+1)}(x _ 0)\neq0$，那么：若$n$是偶数，那么$x _ 0$不是$f$的极值点；若$n$是奇数，那么当$f^{(n+1)}(x _ 0)>0$，$x _ 0$是一个极小值点，当$f^{(n+1)}(x _ 0)<0$，$x _ 0$是一个极大值点。

定理2（必要条件）：设定义在$\Omega\subseteq\mathbb R^n$上的函数$f\in C^1$，若$\boldsymbol x _ 0$是极小值点，那么在$\boldsymbol x _ 0$处的任何可行方向(feasible direction) $\boldsymbol d\in\mathbb R^n$，都有$\nabla f(\boldsymbol x _ 0)^\mathsf T\boldsymbol d\geqslant0$；进而，如果$\boldsymbol x _ 0$是$\Omega$的一个内点，那么$\nabla f(\boldsymbol x _ 0)=0$。

第二个论断是微积分中比较基本的命题。对于第一个论断，我们可以延拓$f$到一个包含$\Omega$的开集$U$中且使得$f$在$\boldsymbol x _ 0$可微，此时方向导数均非负。而对于可微函数，方向$\boldsymbol d$的方向导数可表示为$\nabla f(\boldsymbol x _ 0)^\mathsf T\boldsymbol d$。

定理3（必要条件）：设定义在$\Omega\subseteq\mathbb R^n$上的函数$f\in C^1$，若$\boldsymbol x _ 0$是极小值点，那么对任何满足$\nabla f(\boldsymbol x _ 0)^\mathsf T \boldsymbol d=0$的方向我们都有$\boldsymbol d^\mathsf T\nabla^2f(\boldsymbol x _ 0)\boldsymbol d\geqslant0$；进而，如果$\boldsymbol x _ 0$是$\Omega$的一个内点，那么总有$\boldsymbol d^\mathsf T\nabla^2f(\boldsymbol x _ 0)\boldsymbol d\geqslant0$。

类似地，我们可以延拓$f$使得$\boldsymbol x _ 0$是一个内点。由Taylor定理，$f(\boldsymbol x _ 0+\boldsymbol d)-f(\boldsymbol x _ 0)=\boldsymbol d^\mathsf T\nabla^2f(\boldsymbol x _ 0)\boldsymbol d+o(|\boldsymbol d|^2)=|\boldsymbol d|^2(\boldsymbol u^\mathsf T\nabla^2f(\boldsymbol x _ 0)\boldsymbol u+o(1))$，可以看到，当$|\boldsymbol d|\to0$，$f(\boldsymbol x _ 0+\boldsymbol d)-f(\boldsymbol x _ 0)$与$\boldsymbol d^\mathsf T\nabla^2 f(\boldsymbol x _ 0)\boldsymbol d$同号，于是得到该定理。

定理4（充分条件）：设定义在$\Omega\subseteq\mathbb R^n$上的函数$f\in C^1$，果$\boldsymbol x _ 0$是$\Omega$的一个内点；若$\nabla f(\boldsymbol x _ 0)=0$且$\nabla^2f(\boldsymbol x _ 0)$是正定矩阵，那么$\boldsymbol x _ 0$是一个（严格）极小值点。

凸函数的一些结果

如果有凸性假设，很多极值将变成最值。

定理5：Jensen不等式$f(\sum \alpha _ ix _ i)\leqslant\sum\alpha _ if(x _ i)$；连续性$f\in C(\Omega^\circ)$；线性运算下封闭，即当$f,g$凸时$f+g$和$cf$也是凸的；$\{x\in\Omega\mid f(x)\leqslant c\}$是凸集。

这个定理是微积分中的常规内容了，下面的定理6也是。

定理6：设$f\in C^1$，那么$f$是凸函数当且仅当总有$f(\boldsymbol y)\geqslant f(\boldsymbol x)+\nabla f(\boldsymbol x)^\mathsf T(\boldsymbol y-\boldsymbol x)$。

这个定理可以看作是原始定义的一个对偶刻画。原始定义是说两个点之间的线性插值总是凸函数的过量估计，而这个定理说的是用局部导数线性近似总是凸函数的不足估计。

定理7：设$f\in C^2$，那么$f$是$\Omega$（包含至少一个内点）上的凸函数当且仅当$\nabla^2 f$总是半正定的。

定理7‘：设$f\in C^2$，若$\nabla^2 f$总是正定的，那么$f$是严格凸函数。

定理8：设$f$是凸函数，则$f$的最小值点构成一个凸集，且任何极小值点都是最小值点。

第一个命题是因为$\{x\mid f(x)\leqslant c\}$总是凸集，第二个论断是显然的。

定理9：设$f\in C^1$是凸函数，若存在$\boldsymbol x _ 0$使得$\nabla f(\boldsymbol x _ 0)^\mathsf T(\boldsymbol x-\boldsymbol x _ 0)\geqslant0$，那么（由定理5）$\boldsymbol x _ 0$是最小值点。

定理10：设$f$是定义在紧致的凸集上的凸函数，如果有最大值，那么必在定义域的一个顶点取到。

基本的下降(descent)方法

迭代的下降方法(Iterative descent algorithms)：迭代，意味着算法将产生一列点，每个点基于前一个点计算得到；下降，每个新的点上的对应函数值总比原来的点要小。

定义：设$x _ k\to x$，那么$\{x _ k\}$收敛的阶数(order of convergence)定义为满足某些条件的非负数$p$的上确界，具体如下：
$0\leqslant\limsup _ {k\to\infty}\frac{|x _ {k+1}-x|}{|x _ k-x|^p}=\beta<+\infty.$ 若$p=1$且$\beta<1$，一般将这个序列称作线性收敛(linear convergence)；而当$p>1$或$p=1,\, \beta=0$时称作超线性收敛(super-linear convergence)。

注：如果序列以阶数$p$收敛，那么不难证明上式在$p'<p$时也成立，因而定义里是用上确界来定义。

我们讨论的几乎所有下降算法都有一个基本的底层结构。从一个初始点出发；根据一定条件选择移动的方向；然后在这个方向上移动使得函数能取得一个相对小的值。在这个新的点上计算新的方向，然后不断重复这些步骤。诸 算法（最速下降法、牛顿法等）之间的主要区别在于运动方向的选择。一旦做出选择，算法一般都会要求移动到相应线上的最小值点。

确定给定线上的最小点的过程称为线搜索。 由于线搜索实际上是求解一维极小化问题的过程，因此也称为一维搜索。 在本章中，高维最小化问题通常通过执行一系列连续的线搜索来解决。

线搜索算法

我们可以根据可知信息的多少选择不同的算法。如果连函数的导数都不知道，但知道它是单峰的，那么就可以用下面的黄金分割法来搜索；如果能知道二阶导数，那么就可以用牛顿法。

然而，很多时候要令人满意地解决一维搜索的问题是困难的，或者是要付出相当的代价。在本章最后将会给出实用的非精确线搜索的方法。

黄金分割法

黄金分割法是一种只需知道函数值的信息而不需要知道导数相关的信息就可以应用的算法，对要优化的函数的要求仅仅为它是单峰的(unimodal)，即，存在最小值点$x^\ast$，在它左边函数递减，右边递增。对于单峰的函数，这种方法的做法是依次取一系列点，每一次都得到一个缩短的区间，使得最小值点总落在这个区间内；当区间缩短到可以容忍的长度时，在里面随意取一点就认为它是函数的最小值点。

对于单峰函数，我们要用到的是：第一，函数的最小值点唯一；第二，设$\lambda,\mu\in[a,b] \, (\lambda<\mu)$使得$f(\lambda)\leqslant f(\mu)$，那么$x^\ast\in[a,\mu]$，同理$f(\lambda)\geqslant f(\mu)$可得$b^\ast\in[\lambda,b]$；第三，这点其实包含在第二点了，就是$f(\lambda)=f(\mu)$得$x^\ast\in[\lambda,\mu]$。

黄金分割法每次迭代得到的缩小版区间$[a _ {k+1},b _ {k+1}]$总是上一步区间$[a _ k,b _ k]$长度的0.618比例。

设$(b _ k-a _ k)/(b _ {k+1}-a _ {k+1})\equiv \alpha$，每次我们在区间$[a _ k,b _ k]$内取两个点$\lambda _ k,\mu _ k$计算函数值，根据上面得第二点性质来得到$[a _ {k+1},b _ {k+1}]$，这样$[a _ {k+1},b _ {k+1}]=[\lambda _ k,b _ k]$或者$[a _ {k+1},b _ {k+1}]=[a _ k,\mu _ k]$。$\lambda _ k,\mu _ k$的选择会使得$\lambda _ {k+1}$或者$\mu _ {k+1}$中的一个恰好在$\{\lambda _ k,\mu _ k\}$之中，这样每次迭代只需要再多计算一次函数值即可。具体是，如果$f(\lambda _ k)>f(\mu _ k)$那么$[a _ {k+1},b _ {k+1}]=[\lambda _ k,b _ k]$，$\lambda _ {k+1}=\mu _ k$，$\mu _ {k+1}$再取自$[\lambda _ {k+1},b _ {k+1}]$；如果$f(\lambda _ k)\leqslant f(\mu _ k)$，那么$[a _ {k+1},b _ {k+1}]=[a _ k,\mu _ k]$，$\mu _ {k+1}=\lambda _ k$，$\lambda _ {k+1}$再取自$[a _ {k+1},\mu _ {k+1}]$。

我们可以推得，满足上面迭代过程要求的$\alpha$就是黄金分割比0.618，即$\alpha^2+\alpha-1=0$的正根。于是我们得到了如下算法：

1. 选择可接受的最大不确定度$l>0$，令$[a _ 1,b _ 1]=[a,b]$，$\lambda _ 1=a _ 1+(1-\alpha)(b _ 1-a _ 1)$，$\mu _ 1=a _ 1+\alpha(b _ 1-a _ 1)$，令$k=1$。
2. 如果$b _ k-a _ k\leqslant l$，则停止算法，最小值点在$[a _ k,b _ k]$中；否则继续算法。
3. 如果$f(\lambda _ k)>f(\mu _ k)$，令$[a _ {k+1},b _ {k+1}]=[\lambda _ k,b _ k]$，$\lambda _ {k+1}=\mu _ k$，$\mu _ {k+1}=a _ {k+1}+\alpha(b _ {k+1}-a _ {k+1})$，并计算$f(\mu _ {k+1})$。
4. 如果$f(\lambda _ k)\leqslant f(\mu _ k)$，令$[a _ {k+1},b _ {k+1}]=[a _ k,\mu _ k]$，$\mu _ {k+1}=\lambda _ k$，$\lambda _ {k+1}=a _ {k+1}+(1-\alpha)(b _ {k+1}-a _ {k+1})$，并计算$f(\lambda _ {k+1})$。
5. $k\leftarrow k+1$并回到步骤2.

当一阶导数可知

此时可以使用迭代：
$x _ {k+1}=x _ k-f'(x _ k)\frac{x _ {k-1}-x _ k}{f'(x _ {k-1})-f'(x _ k)}.$

这十分类似于下面提到的牛顿法，只是牛顿法里面的二阶导被上面的分式近似了。如果收敛，收敛阶数是1.618.

当二阶导数可知

此时就有著名的牛顿法(Newton's method)可用了。牛顿法想法是构造一个$f$的二阶近似，即$q(x)=f(x _ k)+f'(x _ k)(x-x _ k)+\frac12f''(x _ k)(x-x _ k)^2$，然后$x _ {k+1}$取$q'(x)=0$的解，即$0=f'(x _ k)+f''(x _ k)(x _ {k+1}-x _ k)$，于是
$x _ {k+1}=x _ k-\frac{f'(x _ k)}{f^{\prime\prime}(x _ k)}.$
可以看到，令$g(x)=f'(x)$这个方法就可以看作是求解$f'(x)=0$的迭代算法；$x _ {k+1}=x _ k-\frac{g(x)}{g'(x)}$。牛顿法的收敛阶数是2（如果收敛）。

最速下降法(Method of steepest descent)

最小化一个多元函数的最古老、最广为人知的方法之一就是最陡下降法/最速下降法。因其有令人满意的理论分析，它在理论上地位重要。很多现代算法的出发点正是从基本的最陡下降法修改，使新算法有更好的收敛性。因而，最陡下降法不仅是在遇到新问题时首先被想到使用的标准技术，也是衡量其它方法的一个标杆。

方法的迭代步骤是
$\boldsymbol x _ {k+1}=\boldsymbol x _ k-\alpha _ k \boldsymbol g _ k,$
其中$\boldsymbol g _ k=\nabla f(\boldsymbol x _ k)$，$\alpha _ k$选择是或能最小化$f(\boldsymbol x _ k-\alpha \boldsymbol g _ k)$的非负实数。就是说，我们在方向$-\boldsymbol g _ k$上进行线搜索（因为在微积分中我们已知梯度$\boldsymbol g _ k$是函数增加最快的方向，那么反方向$-\boldsymbol g _ k$就是函数减小最快的方向），找到的最小值点就是$\boldsymbol x _ {k+1}$。这个算法如果得到一个有界$\{\boldsymbol x _ k\}$，那么将收敛至一个驻点。

二次函数的情形

最陡下降法的分析可以简单来看其应用在优化二次函数时的表现。我们考虑优化函数$f(\boldsymbol x)=\frac12\boldsymbol x^\mathsf TQ\boldsymbol x-\boldsymbol b^\mathsf T\boldsymbol x$，这里$Q$是正定矩阵。此时最优解有闭式解，$\boldsymbol x^\ast$满足$Q\boldsymbol x^\ast=\boldsymbol b$。同时，我们也可以考虑函数$E(\boldsymbol x)=\frac12(\boldsymbol x-\boldsymbol x^\ast)^\mathsf TQ(\boldsymbol x-\boldsymbol x^\ast)$，那么$E(\boldsymbol x)=f(\boldsymbol x)+\frac12\boldsymbol x^\ast{}^\mathsf TQ\boldsymbol x$，即$E$和$f$仅相差一个常数。

不难推知，此时的迭代步骤为：梯度向量$\boldsymbol g _ k=Q\boldsymbol x _ k-\boldsymbol b$，$\alpha _ k=\frac{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}{\boldsymbol g _ k^\mathsf TQ\boldsymbol g _ k}$，故
$\boldsymbol x _ {k+1}=\boldsymbol x _ k-\frac{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}{\boldsymbol g _ k^\mathsf TQ\boldsymbol g _ k}\boldsymbol g _ k.$

关于此时的收敛，有
$E(\boldsymbol x _ {k+1})\leqslant\Big(\frac{\lambda _ n-\lambda _ 1}{\lambda _ n+\lambda _ 1}\Big) ^2E(\boldsymbol x _ k).$
其中$\lambda _ 1,\lambda _ n$分别是$Q$的最小最大特征值。可以看到，如果$\lambda _ 1=\lambda _ n$，那么收敛一步瞬间完成。但是，即使$n-1$个特征值全相等、一个特征值和它们相去甚远，收敛就可能很慢了。就是说，一个大小不正常的特征值会极大影响最陡下降法的效率。注意到这也完全可以用条件数来表述，条件数极大时影响收敛。

牛顿法(Newton’s method)

和一维时类似，想法是构造一个$f$的二阶近似，即$q(\boldsymbol x)=f(\boldsymbol x _ k)+\nabla f(\boldsymbol x _ k)(\boldsymbol x-\boldsymbol x _ k)+\frac12(\boldsymbol x-\boldsymbol x _ k)^\mathsf T\nabla^2f(\boldsymbol x _ k)(\boldsymbol x-\boldsymbol x _ k)$，然后$x _ {k+1}$取$\nabla q(\boldsymbol x)=\boldsymbol 0$的解，即
$\boldsymbol x _ {k+1}=\boldsymbol x _ k-(\nabla^2f(\boldsymbol x _ k))^{-1}\nabla f(\boldsymbol x _ k).$
一样，如果距离某驻点足够近，那么将以阶数2收敛。

坐标下降法(Coordinate descent methods)

这种方法有时颇为实用，因为易于实现。然而，一般情况下，其收敛性能不如最陡下降。

这种方法基本做法是每次只优化一个$\boldsymbol x$的分量：设$\boldsymbol x=(x _ 1,\dots,x _ n)$，沿坐标$x _ i$下降的意思是$\min _ {x _ i}f(x _ 1,\dots,x _ n)$。如何顺序执行这种下降步骤有多种方式。循环坐标下降(cyclic coordinate descent)这一算法就是下标循环地优化$f$，就是说$x _ 1$先，然后$x _ 2$直到$x _ n$，然后回到$x _ 1$重新开始重复。类似地，可以有Aitken双扫法(Aitken double sweep method)，依次找完$x _ 1,\dots,x _ n$后逆序按$x _ {n-1},\dots,x _ 1$来找。这两种方法无需知道$f$的梯度信息来选择下降的坐标。如果$f$的梯度信息可用，那么也有根据梯度来作出选择的方案。一种较为知名的是Gauss−Southwell Method，每次选择梯度向量里（绝对值）最大的那个分量来进行下降。还有一种随机化策略，即每一步都随机选择一个坐标进行下降。

实用非精确线搜索

在最速下降法（以及一般的线搜索问题）中要找到使$g(\alpha)=f(\boldsymbol x _ k+\alpha\boldsymbol d _ k)$ ($\alpha>0$)的最小值点，然而这点很多时候太难做到了。即使是极小值点也或许需要大量地计算$f$甚至还要$\nabla f$，更实用的方法是采取非精确的线搜索来确定$\alpha$，使得用尽可能少的代价达到充分减小$f$的目标。以下均假设$f$足够光滑。

要减小$f$，自然要做到$f(\boldsymbol x _ k+\alpha\boldsymbol d _ k)<f(\boldsymbol x _ k)$，但只是要做到这个又太过容易。对一个二次函数，就算从初始点一直按同一个方向直接去往最小值点，如果步长指数减小，那么永远也到不了最小值点，即使函数值一直在下降。我们需要更强一点的条件。

Wolfe条件

一个知名的条件是说，目标函数起码要有足够的下降，足够一词可以用下面的不等式衡量：
$f(\boldsymbol x _ k+\alpha\boldsymbol d _ k)\leqslant f(\boldsymbol x _ k)+c _ 1\alpha (\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k).$其中$c _ 1$是一个$(0,1)$中的常数，实际通常取一个较小的数例如$c _ 1=10^{-4}$。这一不等式常称作Armijo条件。其大意是$f$起码的减小与步长$\alpha$和方向导数$\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k$成比例。

上图形象展示了这一条件（即在虚线下方）。不等式的右边可看出是关于$\alpha$的斜率为负数的线性函数，记为$l(\alpha)$，斜率是$c _ 1(\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k)$，由于$c _ 1\in(0,1)$，同时$g'(0)=\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k$，可知$\alpha$充分小的时候$l(\alpha)$总在$g(\alpha)$上方。

在这一条件的基础上我们又希望$\alpha$别太小，因此引入另外一个曲率条件：
$\nabla f(\boldsymbol x _ k+\alpha\boldsymbol d _ k)^\mathsf T\boldsymbol d _ k\geqslant c _ 2\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k.$其中$c _ 2$是一个$(c _ 1,1)$中的常数，例如在牛顿或拟牛顿法中常取$0.9$，共轭梯度法中常取$0.1$。左边正是$g'(\alpha)$，所以这个条件要求的是$g'$在$\alpha$的值应大于在$0$点处的值的$c _ 2$倍。不难理解，因为$g'(\alpha)$远小于$0$时可较为安全地增大$\alpha$使$f$下降。下图形象展示了函数曲线满足这一条件的部分。

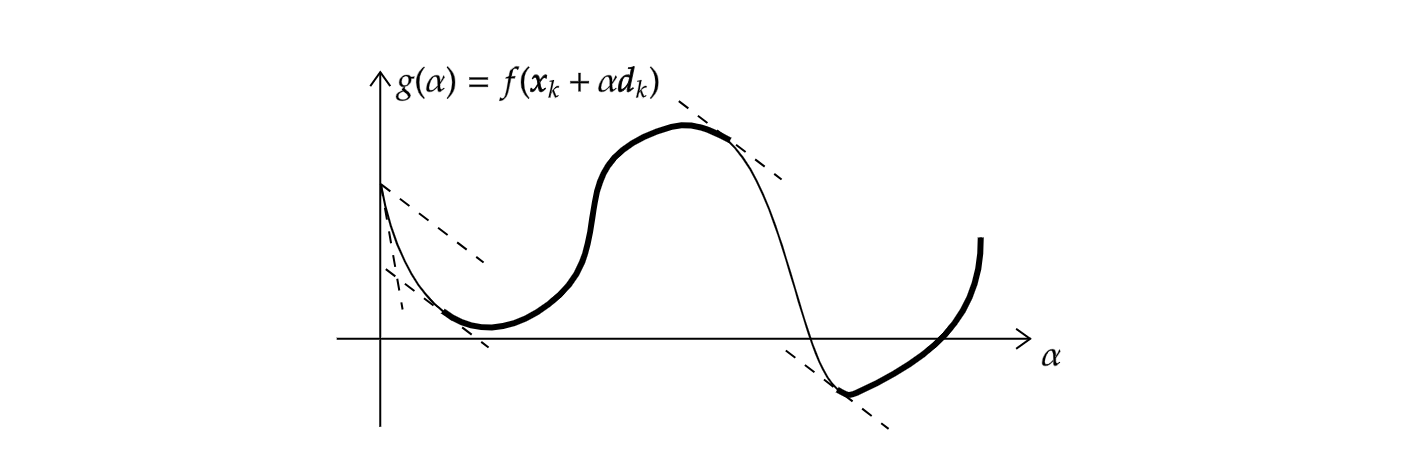
上面的两个条件并称Wolfe条件。把它们写在一起，
$\begin{aligned}f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)&\leqslant f(\boldsymbol x _ k)+c _ 1\alpha _ k (\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k),\\ \nabla f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)^\mathsf T\boldsymbol d _ k&\geqslant c _ 2\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k.\end{aligned}\begin{aligned}f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)&\leqslant f(\boldsymbol x _ k)+c _ 1\alpha _ k (\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k),\\ \nabla f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)^\mathsf T\boldsymbol d _ k&\geqslant c _ 2\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k.\end{aligned}$其中$0<c _ 1<c _ 2<1$。此外还有强Wolfe条件：$\alpha _ k$满足
$\begin{aligned}f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)&\leqslant f(\boldsymbol x _ k)+c _ 1\alpha _ k (\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k),\\ |\nabla f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)^\mathsf T\boldsymbol d _ k|&\leqslant c _ 2|\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k|.\end{aligned}\begin{aligned}f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)&\leqslant f(\boldsymbol x _ k)+c _ 1\alpha _ k (\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k),\\ |\nabla f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)^\mathsf T\boldsymbol d _ k|&\leqslant c _ 2|\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k|.\end{aligned}$只是加了个绝对值号，意味着$g'(\alpha)$不能是太大的正数了。这也排除了一些离驻点较远的点。

可以证明若$f\in C^1$、$\boldsymbol d _ k$是一个下降方向、$f$在这个方向有下界时，存在满足（强）Wolfe条件的$\alpha$区间。

Goldstein条件

另一个类似的条件是Goldstein条件：
$f(\boldsymbol x _ k)+(1-c)\alpha _ k\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k\leqslant f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)\leqslant f(\boldsymbol x _ k)+c\alpha _ k\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k.$其中$c$满足$0<c<1-c<1$。右边的不等式与上面第一个一致，左边的不等式则排除了较小的$\alpha$。与Wolfe条件相比，Goldstein条件有可能会把满足$g'(\alpha)=0$的点都排除掉。

算法

先看简单的backtracking算法。

Backtracking线搜索算法：初始化$\alpha$，$\rho,c\in(0,1)$。

1. 若$f(\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k)\leqslant f(\boldsymbol x _ k)+c _ 1\alpha _ k (\nabla f(\boldsymbol x _ k)^\mathsf T\boldsymbol d _ k)$，取$\alpha _ k=\alpha$，算法终止；
2. 否则，$\alpha\leftarrow\rho\alpha$，回到第1步；

下面再给出一个能确保给出满足强Wolfe条件的线搜索算法。仍假设$f\in C^1$、$\boldsymbol d _ k$是一个下降方向、$f$在这个方向有下界。先简要描述该算法。

先指定一个步长的上限$\alpha _ {\max}$，我们在$(0,\alpha _ {\max})$中找出一个满足强Wolfe条件的$\alpha _ \ast$：在这个区间内取一个递增的${\alpha _ i}$，它们将$(0,\alpha _ {\max})$划分成很多小区间，然后从左到右确定哪个小区间内包含有满足条件的$\alpha$。我们利用三个依据来判断$(\alpha _ {i-1},\alpha _ i)$内含有这个$\alpha$：第一，$g(\alpha _ i)>g(0)+c _ 1\alpha _ i g'(0)$，即不满足第一条条件；第二，$g(\alpha _ i)\geqslant g(\alpha _ {i-1})$；第三，$g'(\alpha _ i)\geqslant0$。如果这三个都不成立，即$\alpha _ i$满足第一条条件、和前一个$\alpha _ {i-1}$比使函数下降、导数为负，那么我们可以继续向前搜索，直到找出包含所需$\alpha _ \ast$的$(\alpha _ {i-1},\alpha _ {i})$。然后，再从$(\alpha _ {i-1},\alpha _ i)$里面不停缩小区间长度，用同样的测试手段。

线搜索算法：初始化$\alpha _ 0=0$，$\alpha _ {\max}>0$，$\alpha _ 1\in(\alpha _ 0,\alpha _ {\max})$，$i=1$；

1. 计算$g(\alpha _ i)$，若$g(\alpha _ i)>g(0)+c _ 1\alpha _ i g'(0)$，或$g(\alpha _ i)\geqslant g(\alpha _ {i-1})$，则$\alpha _ \ast=\mathtt{zoom}(\alpha _ {i-1},\alpha _ i)$，算法终止；
2. 否则，计算$g'(\alpha _ i)$：
   若$|g'(\alpha _ i)|\leqslant-c _ 2 g'(0)$，则$\alpha _ \ast=\alpha _ i$，算法终止；
   否则，若$g'(\alpha _ i)\geqslant0$，则$\alpha _ \ast=\mathtt{zoom}(\alpha _ i,\alpha _ {i-1})$，算法终止；
3. 取$\alpha _ {i+1}\in(\alpha _ i,\alpha _ {\max})$，令$i\leftarrow i+1$，回到步骤1.

其中$\mathtt{zoom}$函数能返回包含$\alpha _ \ast$的小区间内的$\alpha _ \ast$，接收两个参数，设为$a,b$，那么$\mathtt{zoom}(a,b)$的调用必须：1. $a,b$构成的区间包含$\alpha _ \ast$；2. $a$是当前已测试的诸$\alpha$中满足Wolfe强条件的第一条的、使得函数值最小的；3. 若$g'(a)$为正，则$b<a$，若为负，则$b>a$。

$\mathtt{zoom}$函数：

1. 取位于$a,b$之间的$\alpha _ j$并计算$g(\alpha _ j)$；
2. 若$g(\alpha _ j)>g(0)+c _ 1\alpha _ jg'(0)$或$g(\alpha _ j)>g(a)$，则令$b=\alpha _ j$，回到步骤1；
3. 否则，计算$g'(\alpha _ j)$：
   若$|g'(\alpha _ j)|\leqslant -c _ 2g'(0)$，则$\alpha _ \ast=\alpha _ j$，算法终止；
   否则，若$g'(\alpha _ j)(b-a)\geqslant0$，则令$b=a$，$a=\alpha _ j$，回到步骤1；若小于$0$，则令（$b=b$，）$a=\alpha _ j$，回到步骤1.