共轭梯度法

在共轭梯度法(conjugate gradient method)之前，先来看共轭方向法(conjugate direction method)。共轭方向法可以一定程度看作是介于最速下降法和牛顿法之间的方法。出发点是想要比最速下降法收敛要快，但又不必要有牛顿法那么多的信息要求和储存、计算条件。

共轭方向法先是用于分析二次函数的优化\min\frac12\boldsymbol x^\mathsf TQ\boldsymbol x-\boldsymbol b^\mathsf T\boldsymbol x，其中Q正定。如果能对二次函数有一定结果那么就可以通过一定的近似得到一般问题的推广。在最优解的附近，一般认为已经是近似二次的问题了，收敛也将和二次问题类似。这种算法的出现表明，在二次函数优化问题上的分析很多时候可以适用于非常实际的一般问题，共轭方向法尤其是共轭梯度法在解决它们时尤为有效，因而这种方法被视作是最好的优化方法之一。

共轭方向法

定义：向量\boldsymbol d _ 1,\boldsymbol d _ 2称作是Q-正交的（Q为对称矩阵），或称作是关于Q共轭的，如果\boldsymbol d _ 1^\mathsf TQ\boldsymbol d _ 2=0.

命题：1. 相互Q-正交的非零向量\boldsymbol d _ 0,\boldsymbol d _ 1,\dots,\boldsymbol d _ k是线性无关的。2. 属于对称矩阵Q的不同特征值的两个特征向量是Q-正交的。

第一条，显然任何一个\boldsymbol d都不能被其余的线性表示。第二条，由于是特征向量，Q-正交等价于普通的正交，线性代数里，属于不同特征值的特征向量当然正交。

从二次函数出发推导

二次函数的优化问题：\min\frac12\boldsymbol x^\mathsf TQ\boldsymbol x-\boldsymbol b^\mathsf T\boldsymbol x，其中Q正定，这个问题的唯一解就是线性方程Q\boldsymbol x=\boldsymbol b的解，就是说优化二次函数就是解一个线性方程。假设我们有n个非零的Q-正交向量\boldsymbol d _ 0,\boldsymbol d _ 1,\dots,\boldsymbol d _ {n-1}，那么由于它们线性独立，二次函数最优解\boldsymbol x^\ast可以被它们线性表示：\boldsymbol x^\ast=\alpha _ 0\boldsymbol d _ 0+\dots\alpha _ {n-1}\boldsymbol d _ {n-1}，我们事实上可以求出这些系数。\alpha _ i=\boldsymbol d _ i^\mathsf TQ\boldsymbol x^\ast\mathbin/\boldsymbol d _ i^\mathsf TQ\boldsymbol d _ i=\boldsymbol d _ i^\mathsf T\boldsymbol b\mathbin/\boldsymbol d _ i^\mathsf TQ\boldsymbol d _ i，于是
\boldsymbol x^\ast=\sum _ {n=0}^{n-1}\frac{\boldsymbol d _ i^\mathsf T\boldsymbol b}{\boldsymbol d _ i^\mathsf TQ\boldsymbol d _ i}\boldsymbol d _ i.到这里就可以看出这种方法的用意了。将\boldsymbol x^\ast用一组基线性表示，而表示的系数要可以求出来，所以我们需要一组正交基，以便方便求出；另一方面，一般的正交基表示出来系数会带有未知的\boldsymbol x^\ast，所以我们用Q-正交基，这样最后\boldsymbol x^\ast会被化成\boldsymbol b，所有系数都变成已知的了。

\boldsymbol x^\ast的这种线性表示可以看作是一种迭代算法执行n次、每次加上一个\alpha _ i\boldsymbol d _ i的结果。基于这种想法，我们就可以得到基本的共轭方向法。

定理（共轭方向）：对于二次函数。设有n个非零的Q-正交向量\boldsymbol d _ 0,\boldsymbol d _ 1,\dots,\boldsymbol d _ {n-1}，设从\boldsymbol x _ 0出发，进行如下迭代：
\begin{gathered}\boldsymbol x _ {k+1}=\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k,\\\alpha _ k=-\frac{\boldsymbol g _ k^\mathsf T\boldsymbol d _ k}{\boldsymbol d _ k^\mathsf TQ\boldsymbol d _ k},\\\boldsymbol g _ k=Q\boldsymbol x _ k-\boldsymbol b.\end{gathered}那么n步后将收敛至\boldsymbol x^\ast，即Q\boldsymbol x=\boldsymbol b的解，这表明\boldsymbol x _ n=\boldsymbol x^\ast。

.

证明是完全一样的。只需将\boldsymbol x^\ast-\boldsymbol x _ 0用基线性表示再求出系数，并注意到\boldsymbol d _ k^\mathsf TQ(\boldsymbol x _ k-\boldsymbol x _ 0)=0即可。

共轭方向法的理解

定理：对于二次函数。设有n个非零的Q-正交向量\boldsymbol d _ 0,\boldsymbol d _ 1,\dots,\boldsymbol d _ {n-1}，k步共轭方向法后得到\boldsymbol x _ k，这个点是直线\boldsymbol x=\boldsymbol x _ {k-1}+\alpha\boldsymbol d _ {k-1}\, (\alpha\in\mathbb R)上使f(\boldsymbol x)最小的点，也是空间\boldsymbol x _ 0+\mathrm{span}\{\boldsymbol d _ i\} _ {i=0}^{k-1}上使得f(\boldsymbol x)最小的点。

考虑其证明。只需证\boldsymbol x _ k是\boldsymbol x _ 0+\mathrm{span}\{\boldsymbol d _ i\} _ {i=0}^{k-1}上的最小值点即可，因为这个空间包含直线\boldsymbol x=\boldsymbol x _ {k-1}+\alpha\boldsymbol d _ {k-1}。注意到f的凸性，对任意\boldsymbol y\in\boldsymbol x _ 0+\mathrm{span}\{\boldsymbol d _ i\} _ {i=0}^{k-1}，有f(\boldsymbol y)\geqslant f(\boldsymbol x _ k)+\nabla f(\boldsymbol x _ k)^\mathsf T(\boldsymbol y-\boldsymbol x _ k)，于是只要能证明\nabla f(\boldsymbol x _ k)^\mathsf T(\boldsymbol y-\boldsymbol x _ k)=0即可（即\boldsymbol g _ k\perp\mathrm{span}\{\boldsymbol d _ i\} _ {i=0}^{k-1}）。k=1时显然，因为\{\boldsymbol d _ i\} _ {i=0}^{k-1}=\varnothing。假设已有\boldsymbol g _ k\perp\mathrm{span}\{\boldsymbol d _ i\} _ {i=0}^{k-1}，下证这对k+1也成立。\boldsymbol g _ {k+1}=Q\boldsymbol x _ {k+1}-\boldsymbol b=Q\boldsymbol x _ k+\alpha _ kQ\boldsymbol d _ k-\boldsymbol b=\boldsymbol g _ k+\alpha _ kQ\boldsymbol d _ k，对于小于k的下标i，\boldsymbol d _ i^\mathsf T\boldsymbol g _ {k+1}=\boldsymbol d _ i^\mathsf T\boldsymbol g _ k+\alpha _ k\boldsymbol d _ i^\mathsf TQ\boldsymbol d _ k，第一项由归纳假设、第二项由Q-正交条件，可知都为0，故只剩\boldsymbol d _ k^\mathsf T\boldsymbol g _ {k+1}=0需证，而这可以通过展开\boldsymbol g _ {k+1}后代入\alpha _ k的定义立得。这就证明了对任何k总有\boldsymbol g _ k\perp\mathrm{span}\{\boldsymbol d _ i\} _ {i=0}^{k-1}。

推论：从证明过程可以看出：对于在\boldsymbol x _ k点处的梯度\boldsymbol g _ k，它和之前的方向正交。即
\boldsymbol g _ k^\mathsf Td _ i=0,\quad \forall\, i<k.
由这个定理显然可以看出\boldsymbol x _ n是f的全局最小值点。共轭方向法从\boldsymbol x _ 0出发，每次迭代是在一个i维子空间中的优化，然后下一次迭代是在一个更大的包含前一步空间的i+1维子空间中的优化，从而迭代n次后即是整个n维空间的全局优化。如下图所示。

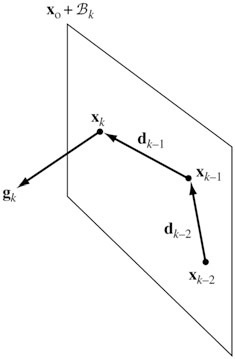
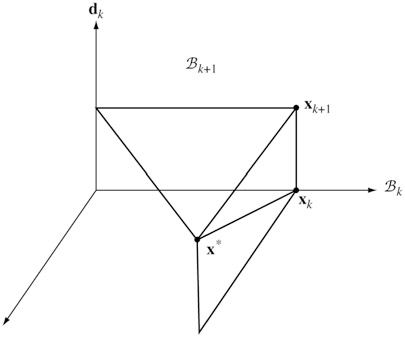
另一方面，若从E(\boldsymbol x)=\frac12(\boldsymbol x-\boldsymbol x^\ast)^\mathsf TQ(\boldsymbol x-\boldsymbol x^\ast)出发来分析（前面提到过E和f只相差一个常数），E可以看作是一种广义欧氏距离，当Q=I _ n时对应普通的欧氏距离。此时\boldsymbol d _ i可以看作是广义的正交基。如下图所示。\boldsymbol x _ k是B _ k上的最小值点，而\boldsymbol x _ {k+1}是B _ {k+1}上的最小值点。因为\boldsymbol d _ k和B _ k广义正交，\boldsymbol x _ {k+1}就可以从\boldsymbol x _ k出发沿直线\boldsymbol d _ k找最小值点得到。n步后到达\boldsymbol x^\ast。

共轭梯度法

共轭梯度法是事先没有给定n个共轭方向的共轭方向法，而是在每步迭代过程中计算得到。

简单讨论。第一，如果\nabla f(\boldsymbol x _ k)提前归零，那么算法终止，无需计算其余的共轭方向。第二，计算新的共轭方向形式简单，因而只比最速下降法复杂少许。第三，因为共轭方向基于梯度，整个算法的过程较为“平均”，就是说每一步得到差不多的优化幅度（寻常的共轭梯度的例子，考虑优化欧氏距离，共轭方向是标准正交基，假设从原点出发，最小值点是(0.01,0.01,0.01,100)，那么前三步的变动都是非常微小的）。这点性质对于共轭梯度法能有效推广到非二次优化的一般问题上十分重要。

共轭梯度的算法：对二次函数。从\boldsymbol x _ 0出发，令\boldsymbol d _ 0=-\boldsymbol g _ 0=\boldsymbol b-Q\boldsymbol x _ 0，迭代算式为
\begin{gathered}\boldsymbol x _ {k+1}=\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k,\\\alpha _ k=-\frac{\boldsymbol g _ k^\mathsf T\boldsymbol d _ k}{\boldsymbol d _ k^\mathsf TQ\boldsymbol d _ k},\\\boldsymbol d _ {k+1}=-\boldsymbol g _ {k+1}+\beta _ k\boldsymbol d _ k,\\\beta _ k=\frac{\boldsymbol g _ {k+1}^\mathsf TQ\boldsymbol d _ k}{\boldsymbol d _ k^\mathsf TQ\boldsymbol d _ k},\\\boldsymbol g _ k=Q\boldsymbol x _ k-\boldsymbol b.\end{gathered}
可以证明，共轭梯度法是一种共轭方向法（只需证明上面的\boldsymbol d _ k都互相Q-正交）。

定理（共轭梯度）：共轭梯度法是一种共轭方向法。如果在\boldsymbol x _ k算法没有终止，那么：

1. \[\mathrm{span}\{\boldsymbol g _ 0,\boldsymbol g _ 1,\dots,\boldsymbol g _ k\}=\mathrm{span}\{\boldsymbol d _ 0,\boldsymbol d _ 1,\dots,\boldsymbol d _ k\}=\mathrm{span}\{\boldsymbol g _ 0,Q\boldsymbol g _ 0,\dots,Q^{k}\boldsymbol g _ 0\};\]

2. \boldsymbol d _ i^\mathsf TQ\boldsymbol d _ j=0；

3. \alpha=\dfrac{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}{\boldsymbol d _ k^\mathsf TQ\boldsymbol d _ k}；
4. \beta _ k=\dfrac{\boldsymbol g _ {k+1}^\mathsf T\boldsymbol g _ {k+1}}{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}.

证明略。

非二次函数的情形

基于二次函数的共轭梯度法可以推广到一般函数上。下面给出两种推广方式。

共轭梯度法1：

1. 初始化\boldsymbol x _ 0，\boldsymbol g _ 0=\nabla f(\boldsymbol x _ 0)，\boldsymbol d _ 0=-\boldsymbol g _ 0。
2. 对k=0,1,\dots,n-1，
   1. 令\boldsymbol x _ {k+1}=\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k，其中\alpha _ k=-\dfrac{\boldsymbol g _ k^\mathsf T\boldsymbol d _ k}{\boldsymbol d _ k^\mathsf T\nabla^2 f(\boldsymbol x _ k)\boldsymbol d _ k}；
   2. 计算\boldsymbol g _ {k+1}=\nabla f(\boldsymbol x _ {k+1})；
   3. 若k<n-1，则令\boldsymbol d _ {k+1}=-\boldsymbol g _ {k+1}+\beta _ k\boldsymbol d _ k，其中\beta _ k=\dfrac{\boldsymbol g _ {k+1}^\mathsf TQ\boldsymbol d _ k}{\boldsymbol d _ k^\mathsf TQ\boldsymbol d _ k}，回到2.1；
3. 将\boldsymbol x _ 0换为\boldsymbol x _ n，回到1.

这种算法的特点在于我们无需进行线搜索，缺点在于我们需要频繁地计算Hesse矩阵\nabla^2 f，也并非全局收敛。

如果进行线搜索来选择\alpha _ k，或是用不同形式的\beta _ k，就有其它算法。第一个提出的是Fletcher–Reeves法，

共轭梯度法2：

1. 初始化\boldsymbol x _ 0，\boldsymbol g _ 0=\nabla f(\boldsymbol x _ 0)，\boldsymbol d _ 0=-\boldsymbol g _ 0。
2. 对k=0,1,\dots,n-1，
   1. 令\boldsymbol x _ {k+1}=\boldsymbol x _ k+\alpha _ k\boldsymbol d _ k，其中\alpha _ k通过线搜索得到，使得f(\boldsymbol x _ k+\alpha\boldsymbol d _ k)最小；
   2. 计算\boldsymbol g _ {k+1}=\nabla f(\boldsymbol x _ {k+1})；
   3. 若k<n-1，则令\boldsymbol d _ {k+1}=-\boldsymbol g _ {k+1}+\beta _ k\boldsymbol d _ k，其中\beta _ k=\dfrac{\boldsymbol g _ {k+1}^\mathsf T\boldsymbol g _ {k+1}}{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}，回到2.1；
3. 将\boldsymbol x _ 0换为\boldsymbol x _ n，回到1.

另外一种重要方法是Polak–Ribiere法，它计算\beta _ k为\beta _ k=\dfrac{(\boldsymbol g _ {k+1}-\boldsymbol g _ k)^\mathsf T\boldsymbol g _ {k+1}}{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}，实验似乎要表现好点。

收敛是可以保证的。每次在第二步k=0时，方向是负梯度，然后按线搜索移动——这就是最速下降法的一步，而k>0时的移动起码不会使f增加，因为最坏的情况也就是不移动，f不变。所以线搜索版本的共轭梯度法是全局收敛的。我们也可以看到第3步重置的意义，这样每n步都至少有一步按梯度计算方向，否则无法保证\boldsymbol d是使f减小的方向。

拟牛顿法(quasi-Newton methods)

拟牛顿法也是可以一定程度看作是介于最速下降法和牛顿法之间的方法。拟牛顿法的想法是将牛顿法中的Hessian的逆用一个近似来替代。

我们假设迭代过程是\boldsymbol x _ {k+1}=\boldsymbol x _ k-\alpha _ kS _ k\nabla f(\boldsymbol x _ k)，其中S _ k是对称矩阵以及\alpha _ k照常地使f(\boldsymbol x _ {k+1})最小。如果S _ k是Hessian的逆，那么这个就是牛顿法，如果是单位阵，那么这个就是最速下降法。

注意，为了使这个迭代算法对于小\alpha _ k时是下降，一般要求S _ k正定。

如果是优化二次函数，那么\alpha _ k有显式解，收敛满足E(\boldsymbol x _ {k+1})\leqslant(\frac{\lambda _ {kn}-\lambda _ {k1}}{\lambda _ {kn}+\lambda _ {k1}})^2E(\boldsymbol x _ k)，其中\lambda _ k表示S _ kQ的特征值。我们可以看到S _ {k}接近Hesse矩阵Q的好处，因为此时\lambda _ k全都接近于1，收敛将会十分迅速。而当优化一般函数时，我们会想类似地做到S _ k接近\nabla^2 f(\boldsymbol x _ k)^{-1}。一种经典的做法是classical modified Newton’s method，其迭代是\boldsymbol x _ {k+1}=\boldsymbol x _ k-\alpha _ k[\nabla^2 f(\boldsymbol x _ 0)]^{-1}\nabla f(\boldsymbol x _ k)，就是说它没有做任何的Hessian近似，只是简单将S _ k设置为常量。显然，这种做法的有效性将依赖于Hessian会不会变化太快。

DFP方法

考虑优化问题
\min f(\boldsymbol x),其中f\in C^2。我们引入一些记号。对两点\boldsymbol x _ {k+1},\boldsymbol x _ k，定义\boldsymbol g _ {k+1}=\nabla f(\boldsymbol x _ {k+1})，\boldsymbol g _ k=\nabla f(\boldsymbol x _ k)，
\boldsymbol s _ k=\boldsymbol x _ {k+1}-\boldsymbol x _ k,\quad \boldsymbol y _ k=\nabla f(\boldsymbol x _ {k+1})-\nabla f(\boldsymbol x _ k).
我们简单来看算法的推导，推导细节复杂，略过，可见另一篇长文推导。近似地，\boldsymbol y _ k\approx \nabla^2 f(\boldsymbol x _ k)\boldsymbol s _ k。我们近似Hessian的逆H _ {k+1}使得等式H _ {k+1}\boldsymbol y _ k=\boldsymbol s _ k成立，且要使得H _ {k+1}正定，这就必须\boldsymbol y _ k^\mathsf T\boldsymbol s _ k>0，这个条件在f严格凸时自动成立，但f没有凸性时则不然，我们需要自己指定这一条件（在精确线搜索时也是自动成立）。

满足条件的这种近似有无穷多，令B _ {k+1}=H _ {k+1}^{-1}，B _ k=H _ k^{-1}，考虑B _ {k+1}为如下优化问题的解：
\begin{aligned}\min _ B{}&\quad\|B-B _ k\|,\\\text{s.t. }&\quad B=B^\mathsf T,\boldsymbol y _ k=B\boldsymbol s _ k.\end{aligned}其中B _ k是正定的，范数可取不同范数，现在取加权Frobenius范数：\|A\| _ W=\|W^\frac12AW^\frac12\| _ F，这里\|\cdot\| _ F则为熟知的Frobenius范数，定义为\|A\|^2 _ F=\mathsf{tr}(A^\mathsf TA)=\sum _ {i,j}a _ {ij}^2；这里我们选择权重矩阵W使得W\boldsymbol y _ k=\boldsymbol s _ k且W\succ 0。此时\|B-B _ k\| _ W=\|W^\frac12(B-B _ k)W^\frac12\| _ F，求解得
B _ {k+1}^{\mathrm{DFP}}=\frac{\boldsymbol y _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}+\Big(I _ n-\frac{\boldsymbol y _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big)B _ k\Big(I _ n-\frac{\boldsymbol s _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big).求逆解得
H _ {k+1}^{\mathrm{DFP}}=H _ k-\frac{H _ k\boldsymbol y _ k\boldsymbol y _ k^\mathsf TH _ k}{\boldsymbol y _ k^\mathsf TH _ k\boldsymbol y _ k}+\frac{\boldsymbol s _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}.这正是下面DFP算法里的更新公式。

.

Davidon-Fletcher-Powell方法，最早的构建Hessian逆的近似的方法，闻名于世。每一步Hessian的逆用两个秩1矩阵的和相加来进行更新，因而这种方式也经常被称作是一种二秩矫正程序(rank two correction procedure)。下面给出DFP算法。

DFP算法：初始化，取正定矩阵H _ 0，初始点\boldsymbol x _ 0，k=0。

1. 令\boldsymbol d _ k=-H _ k\nabla f(\boldsymbol x _ k).

2. 优化\min _ {\alpha\geqslant0}f(\boldsymbol x _ {k}+\alpha \boldsymbol d _ k)得到\alpha _ k,\boldsymbol x _ {k+1}及\boldsymbol s _ k=\alpha _ k\boldsymbol d _ k.

3. 令\boldsymbol y _ k=\nabla f(\boldsymbol x _ {k+1})-\nabla f(\boldsymbol x _ k)，以及
   H _ {k+1}=H _ k-\frac{H _ k\boldsymbol y _ k\boldsymbol y _ k^\mathsf TH _ k}{\boldsymbol y _ k^\mathsf TH _ k\boldsymbol y _ k}+\frac{\boldsymbol s _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}.更新k，若未满足终止条件，回到步骤1。

.

算法值得稍加分析。可以证明若H _ k正定，则H _ {k+1}正定。由Cauchy-Schwarz不等式，
\boldsymbol x^\mathsf TH _ {k+1}\boldsymbol x=\boldsymbol x^\mathsf TH _ k\boldsymbol x+\frac{(\boldsymbol x^\mathsf T\boldsymbol s _ k)^2}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}-\frac{(\boldsymbol x^\mathsf TH _ k\boldsymbol y _ k)^2}{\boldsymbol y _ k^\mathsf TH _ k\boldsymbol y _ k}\geqslant\frac{(\boldsymbol x^\mathsf T\boldsymbol s _ k)^2}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}.要证明上式非负只需证明\boldsymbol y _ k^\mathsf T\boldsymbol s _ k>0。\boldsymbol y _ k^\mathsf T\boldsymbol s _ k=\boldsymbol s _ k^\mathsf T\nabla f(\boldsymbol x _ {k+1})-\boldsymbol s _ k^\mathsf T\nabla f(\boldsymbol x _ k)，回顾算法第二步\boldsymbol s _ k的定义，\alpha _ k的选取是使得\boldsymbol d _ k^\mathsf T\nabla f(\boldsymbol x _ {k+1})=0成立的，而\boldsymbol s _ k,\boldsymbol d _ k共线，这说明\boldsymbol s _ k^\mathsf T\nabla f(\boldsymbol x _ {k+1})=0，\boldsymbol y _ {k}^\mathsf T\boldsymbol s _ k=-\boldsymbol s _ k^\mathsf T\nabla f(\boldsymbol x _ k)=\alpha _ k\nabla f(\boldsymbol x _ k)^\mathsf TH _ k\nabla f(\boldsymbol x _ k)>0（H _ k正定也意味着\alpha _ k为正）。所以，现在已经证明了\boldsymbol x^\mathsf TH _ {k+1}\boldsymbol x\geqslant0，要证明等号不能成立，即证明H _ k^\frac12\boldsymbol x,H _ k^\frac12\boldsymbol y _ k共线与\boldsymbol x,\boldsymbol s _ k垂直不能同时成立。假设前者成立，则\boldsymbol x,\boldsymbol y _ k共线，设\boldsymbol x=\beta\boldsymbol y _ k，那么\boldsymbol s _ k^\mathsf T\boldsymbol x=\beta \boldsymbol s _ k^\mathsf T\boldsymbol y _ k\neq0，这里用到了前面计算过的\boldsymbol y _ k^\mathsf T\boldsymbol s _ k的结果。这表明后者此时不成立，所以H _ {k+1}正定。

上面证明过程里用到了算法的第二步中线搜索相关的条件，这使我们能够得到一个重要结论：\boldsymbol s _ k^\mathsf T\boldsymbol y _ k>0。这个不等式在前面也已经有所提及。事实上，只要\alpha _ k能够让这个结论成立就能够替换掉算法中的\alpha _ k，此时H _ {k+1}正定。

继续分析算法，简单考察其收敛。对于二次函数，k步后有：
\begin{gathered}\boldsymbol s _ i^\mathsf TQ\boldsymbol s _ i=0,\quad 0\leqslant i<j\leqslant k,\\H _ {k+1}Q\boldsymbol s _ i=\boldsymbol s _ i,\quad 0\leqslant i\leqslant k.\end{gathered}我们看到\boldsymbol s _ i都是Q-正交的，且算法沿着\boldsymbol s _ i优化，故而这个方法是共轭方向法！更进一步，如果H _ 0=I _ n，那么这个方法是共轭梯度法！上面第二式表明1是H _ nQ的n个线性独立的特征向量的特征值，这表明H _ n=Q^{-1}。

BFGS方法

BFGS方法可说是所有拟牛顿法中最有效的了。众多实验表明，其表现要优于DFP，因而现今BFGS要用得更多。

DFP算法的推导基于B=H^{-1}，事实上也可以基于H自身来推导，类似地，H _ {k+1}是如下优化问题的解：
\begin{aligned}\min _ H{}&\quad\|H-H _ k\|,\\\text{s.t. }&\quad H=H^\mathsf T,H\boldsymbol y _ k=\boldsymbol s _ k.\end{aligned}和基于B的推导下的优化问题几乎一致，只要把\boldsymbol y _ k,\boldsymbol s _ k互换、B _ k换成H _ k就得到了这里的优化问题。因此只要把解里面的\boldsymbol y _ k,\boldsymbol s _ k互换、B _ k,H _ k互换就能得到另一个问题的解。这里优化得到的解H _ {k+1}就是Broyden-Fletcher-Goldfarb-Shanno算法对应的更新公式。
H _ {k+1}^{\mathrm{BFGS}}=\Big(I _ n-\frac{\boldsymbol s _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big)H _ k\Big(I _ n-\frac{\boldsymbol y _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big)+\frac{\boldsymbol s _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}.当然也可以写出BFGS方法的关于B的更新公式。
B _ {k+1}^{\mathrm{BFGS}}=B _ k-\frac{B _ k\boldsymbol s _ k\boldsymbol s _ k^\mathsf TB _ k}{\boldsymbol s _ k^\mathsf TB _ k\boldsymbol s _ k}+\frac{\boldsymbol y _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}.然而用B来更新并非良策，因为每次迭代需要解B _ k\boldsymbol d _ k=-\nabla f(\boldsymbol x _ k)来得到\boldsymbol d _ k，需要不菲的计算代价。

BFGS算法：初始化，取正定矩阵H _ 0，初始点\boldsymbol x _ 0，阈值\epsilon>0，k=0。

1. 若\|\nabla f(\boldsymbol x _ k)\|\leqslant\epsilon，算法终止；

2. 否则，计算方向\boldsymbol d _ k=-H _ k\nabla f(\boldsymbol x _ k)，

3. 优化\min _ {\alpha\geqslant0}f(\boldsymbol x _ {k}+\alpha \boldsymbol d _ k)得到\alpha _ k,\boldsymbol x _ {k+1}及\boldsymbol s _ k=\alpha _ k\boldsymbol d _ k.

4. 令\boldsymbol y _ k=\nabla f(\boldsymbol x _ {k+1})-\nabla f(\boldsymbol x _ k)，以及
   H _ {k+1}=\Big(I _ n-\frac{\boldsymbol s _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big)H _ k\Big(I _ n-\frac{\boldsymbol y _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big)+\frac{\boldsymbol s _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}.更新k，回到步骤1.

SR1方法

BFGS和DFP的每次更新都是二秩矫正，事实上也可以考虑一秩矫正，推导简易，曾被多次发现。一秩矫正得到的是SR1更新(symmetric-rank-1)。设
H _ {k+1}=H _ k+a _ k\boldsymbol z _ k\boldsymbol z _ k^\mathsf T.这种更新也使得H _ {k+1}保持对称的性质。我们选择a _ k,\boldsymbol z _ k使得H _ {k+1}\boldsymbol y _ k=\boldsymbol s _ k成立，那么\boldsymbol s _ k=H _ {k+1}\boldsymbol y _ k=H _ k\boldsymbol y _ k+a _ k\boldsymbol z _ k\boldsymbol z _ k^\mathsf T\boldsymbol y _ k，与\boldsymbol y _ k作内积得到\boldsymbol y _ k^\mathsf T\boldsymbol s _ k-\boldsymbol y _ k^\mathsf TH _ k\boldsymbol y _ k=a _ k(\boldsymbol z _ k^\mathsf T\boldsymbol y _ k)^2，这一式代入前一式就解出了\boldsymbol z _ k，再代入更新公式就是
H _ {k+1}=H _ k+\frac{(\boldsymbol s _ k-H _ k\boldsymbol y _ k)(\boldsymbol s _ k-H _ k\boldsymbol y _ k)^\mathsf T}{a _ k(\boldsymbol z _ k^\mathsf T\boldsymbol y _ k)^2}=H _ k+\frac{(\boldsymbol s _ k-H _ k\boldsymbol y _ k)(\boldsymbol s _ k-H _ k\boldsymbol y _ k)^\mathsf T}{\boldsymbol y _ k^\mathsf T(\boldsymbol s _ k-H _ k\boldsymbol y _ k)}.可以看到，这种方法不一定能保持H的正定性，仅当\boldsymbol y _ k^\mathsf T(\boldsymbol s _ k-H _ k\boldsymbol y _ k)>0时保持正定，即使这个成立，也可能只是一个很小的正数，就会带来一些数值问题上的困境。

Broyden类

BFGS和DFP都是对称二秩矫正（基于\boldsymbol s _ k, H\boldsymbol y _ k），它们的加权也应是这种类型的更新（对称、二秩、基于\boldsymbol s _ k,H\boldsymbol y _ k），这就是Broyden类(Broyden family)的更新：
H^\phi=(1-\phi)H^{\mathrm{DFP}}+\phi H^{\mathrm{BFGS}}.
\phi取0,1分别得到DFP和BFGS，事实上，这也包含了SR1的更新，对应的\phi为\phi _ k=\frac{\boldsymbol s _ k^\mathsf T\boldsymbol y _ k}{\boldsymbol s _ k^\mathsf T\boldsymbol y _ k-\boldsymbol s _ k^\mathsf T B _ k\boldsymbol y _ k}，这是个不一定在[0,1]中的数。

Broyden类也可以写为如下形式：
H _ {k+1}^\phi=H _ k+\frac{\boldsymbol s _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}-\frac{H _ k\boldsymbol y _ k\boldsymbol y _ k^\mathsf TH _ k}{\boldsymbol y _ k^\mathsf TH _ k\boldsymbol y _ k}+\phi \boldsymbol v _ k\boldsymbol v _ k^\mathsf T=H _ k^{\mathrm{DFP}}+\phi\boldsymbol v _ k\boldsymbol v _ k^\mathsf T,其中
\boldsymbol v _ k=(\boldsymbol y _ k^\mathsf TH _ k\boldsymbol y _ k)^{1/2}\Big(\frac{\boldsymbol s _ k}{\boldsymbol s _ k^\mathsf T\boldsymbol y _ k}-\frac{H _ k\boldsymbol y _ k}{\boldsymbol y _ k^\mathsf TH _ k\boldsymbol y _ k}\Big).可见\phi\geqslant0时也能保持H的正定性，实际中一般总要求\phi\geqslant0以避免不必要的困难。

L-BFGS

最后来看内存受限的拟牛顿法(Limited-memory quasi-Newton methods)，这种方法不储存n\times n的矩阵近似，而是储存一些n维向量来隐式储存矩阵近似，而收敛速率还尚可。在这些方法中，这里只给出L-BFGS方法。可见这是一个基于BFGS法修改得到的。

将BFGS更新写作\boldsymbol x _ {k+1}=\boldsymbol x _ k-\alpha _ kH _ k\nabla f(\boldsymbol x _ k)，其中H _ k更新方式为
H _ {k+1}=V _ k^\mathsf TH _ kV _ k+\rho _ k\boldsymbol s _ k\boldsymbol s _ k^\mathsf T,而这里面
\begin{gathered}\rho _ k=\frac{1}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k},\quad V _ k=I _ n-\rho _ k\boldsymbol y _ k\boldsymbol s _ k^\mathsf T,\\\boldsymbol s _ k=\boldsymbol x _ {k+1}-\boldsymbol x _ k,\quad \boldsymbol y _ k=\nabla f(\boldsymbol x _ {k+1})-\nabla f(\boldsymbol x _ k).\end{gathered}
L-BFGS不储存H _ k，而储存若干组（设为m组）\{\boldsymbol s _ i,\boldsymbol y _ i\}，算法计算方向需要计算H _ k\nabla f(\boldsymbol x _ k)，只需要利用这些\{\boldsymbol s _ i,\boldsymbol y _ i\}以及\nabla f(\boldsymbol x _ k)来计算。一次迭代计算完毕后计算新的\boldsymbol s _ k,\boldsymbol y _ k，并代替储存里的最后的\boldsymbol s _ i,\boldsymbol y _ i。实际中，m取一些适中的值例如3到20就一般能有不错的结果。

在每一次迭代过程，我们有\boldsymbol x _ k，以及m组\{\boldsymbol s _ i,\boldsymbol y _ i\}\, (i=k-m,\dots, k-1)，取定一个矩阵H _ k^0，把这个矩阵当作H _ {k-m}，然后利用H的更新公式计算m次就是L-BFGS的H _ k。下面的算法对这个H _ k计算了H _ k\nabla f(\boldsymbol x _ k)：

算法(L-BFGS two-loop recursion)：

\boldsymbol q\leftarrow\nabla f(\boldsymbol x _ k);
\mathtt{for}\text{ } i=k-1,k-2,\dots,k-m,
\quad\alpha _ i\leftarrow\rho _ i\boldsymbol s _ i^\mathsf T\boldsymbol q;
\quad\boldsymbol q\leftarrow \boldsymbol q-\alpha _ i\boldsymbol y _ i;
\mathtt{end} \mathtt{for}
\boldsymbol r\leftarrow H _ k^0\boldsymbol q;
\mathtt{for}\text{ } i=k-m,k-m+1,\dots,k-1,
\quad\boldsymbol \beta\leftarrow\rho _ i\boldsymbol y _ i^\mathsf T\boldsymbol r;
\quad\boldsymbol r\leftarrow\boldsymbol r+\boldsymbol s _ i(\boldsymbol \alpha _ i-\boldsymbol \beta);
\mathtt{end} \mathtt{for}
\mathtt{return}\text{ } \boldsymbol r=:H _ k\nabla f(\boldsymbol x _ k).

实际中一种H _ k^0的选择常有不错效果：H _ k^0=\gamma _ k I _ n，其中\gamma _ k=\frac{\boldsymbol s _ {k-1}^\mathsf T\boldsymbol y _ {k-1}}{\boldsymbol y _ {k-1}^\mathsf T\boldsymbol y _ {k-1}}。

算法(L-BFGS)：初始化\boldsymbol x _ 0,整数m>0，k=0；

1. 选择H _ k^0，例如\gamma _ k I _ n；
2. 按上面的算法计算\boldsymbol d _ k=-H _ k\nabla f(\boldsymbol x _ k)；
3. 优化\min _ {\alpha\geqslant0}f(\boldsymbol x _ {k}+\alpha \boldsymbol d _ k)得到\boldsymbol x _ {k+1}；
4. 若k>m，从内存中舍弃\{\boldsymbol s _ {k-m},\boldsymbol y _ {k-m} \}；
5. 计算并储存\boldsymbol s _ k=\boldsymbol x _ {k+1}-\boldsymbol x _ k，\boldsymbol y _ k=\nabla f(\boldsymbol x _ {k+1})-\nabla f(\boldsymbol x _ k)；
6. 更新k，若未满足终止条件则回到步骤1。

L-BFGS主要的不足在于在病态条件数(ill-conditioned)的问题中收敛很慢，特别地，在Hessian特征值分布较广的问题中。

与共轭梯度法的联系

最后来看这个联系。令m=1，H _ k^0\equiv I _ n，更新公式变为了
H _ {k+1}=\Big(I _ n-\frac{\boldsymbol s _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big)\Big(I _ n-\frac{\boldsymbol y _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\Big)+\frac{\boldsymbol s _ k\boldsymbol s _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}.当进行精确线搜索时我们总有\boldsymbol d _ k^\mathsf T\nabla f(\boldsymbol x _ {k+1})=0，\boldsymbol s _ k^\mathsf T\nabla f(\boldsymbol x _ {k+1 })=0，于是
\boldsymbol d _ {k+1}=-H _ {k+1}\nabla f(\boldsymbol x _ {k+1})=-\nabla f(\boldsymbol x _ {k+1})+\frac{\boldsymbol s _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\nabla f(\boldsymbol x _ {k+1}).注意到\frac{\boldsymbol s _ k\boldsymbol y _ k^\mathsf T}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\nabla f(\boldsymbol x _ {k+1})=\frac{\boldsymbol y _ k^\mathsf T\nabla f(\boldsymbol x _ {k+1})}{\boldsymbol y _ k^\mathsf T\boldsymbol s _ k}\boldsymbol s _ k=\frac{(\boldsymbol g _ {k+1}-\boldsymbol g _ k)^\mathsf T\boldsymbol g _ {k+1}}{\boldsymbol y _ k^\mathsf T\boldsymbol d _ k}\boldsymbol d _ k=-\frac{(\boldsymbol g _ {k+1}-\boldsymbol g _ k)^\mathsf T\boldsymbol g _ {k+1}}{\boldsymbol g _ k^\mathsf T\boldsymbol d _ k}\boldsymbol d _ k，而分母为\boldsymbol g _ k^\mathsf T\boldsymbol d _ k=\boldsymbol g _ k^\mathsf T(-\boldsymbol g _ k+c\boldsymbol d _ {k-1})=-\boldsymbol g _ k^\mathsf T\boldsymbol g _ k，故
\boldsymbol d _ {k+1}=-\boldsymbol g _ {k+1}+\frac{(\boldsymbol g _ {k+1}-\boldsymbol g _ k)^\mathsf T\boldsymbol g _ {k+1}}{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}\boldsymbol d _ k.
前面提及过Polak–Ribiere法的共轭梯度的更新是：
\boldsymbol d _ {k+1}=-\boldsymbol g _ {k+1}+\beta _ k\boldsymbol d _ k,\quad \beta _ k=\dfrac{(\boldsymbol g _ {k+1}-\boldsymbol g _ k)^\mathsf T\boldsymbol g _ {k+1}}{\boldsymbol g _ k^\mathsf T\boldsymbol g _ k}.故此时两种方法竟等价。