Contents
带约束的优化问题,KKT条件
微积分的教程里已经可以接触到一些用Lagrange乘数法解条件极值的知识和实例。这里我们考虑更一般的带约束优化问题
\begin{aligned}
\min &\quad f(\boldsymbol x)\\
\text{s.t. }&\quad \boldsymbol h(\boldsymbol x)=\boldsymbol 0,\;
\boldsymbol g(\boldsymbol x)\geqslant\boldsymbol 0,\\
&\quad \boldsymbol x\in\Omega.
\end{aligned}其中\boldsymbol h,\boldsymbol g分别是m(\leqslant n),p维映射(并假设f,\boldsymbol h,\boldsymbol g光滑),它们的两个约束称作是函数约束,而\boldsymbol x\in\Omega称作是集合约束。我们一般淡化集合约束的考虑,着重考虑函数约束。这里面有个概念十分重要——active constraint,以后翻译为“积极约束”,指的是函数约束取等时的那些约束(等式约束也就都看作积极约束)。积极约束能够使我们在很多情况下能够把问题划归为更简单的只带等式约束的优化问题:若\boldsymbol x^\ast是局部最优解,那么它当然也是只留下积极约束的优化问题的局部解,这是因为对非积极约束g _ i(\boldsymbol x^\ast)>0,那么在\boldsymbol x^\ast的邻域也有g _ i(\boldsymbol x)>0,所以去掉非积极约束不影响邻域的可行性(feasibility)。进而,如果去掉非积极约束、且将积极约束全部改为等式约束,那么\boldsymbol x^\ast也仍是局部最优解。
带约束优化问题中有知名的Karush-Kuhn-Tucker(KKT)条件:
Karush-Kuhn-Tucker条件:令\boldsymbol x^\ast是上述带约束的优化问题的极小值点,且在该点LICQ (linear independence constraint qualification) 成立,那么存在m维向量\boldsymbol \lambda与p维非负向量\boldsymbol \mu\geqslant 0使得
\begin{gathered}
\nabla f(\boldsymbol x^\ast)-\nabla \boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda-\nabla \boldsymbol g(\boldsymbol x^\ast)\boldsymbol \mu=\boldsymbol 0,\\
\boldsymbol \mu^\mathsf T\boldsymbol g(\boldsymbol x^\ast)=0.
\end{gathered}
后面再给出解释与证明,首先做一些准备工作。
切平面
这一节需要回顾一些微积分的内容。可根据情况适当跳过。
我们知道,m个方程\boldsymbol h(\boldsymbol x)=\boldsymbol 0通常给出了一个n-m维的曲面,而曲面的点上的切平面(tangent plane)是重要研究对象。设曲面由参数方程\boldsymbol x=\boldsymbol x(\boldsymbol t)(\boldsymbol t\in\mathbb R^{n-m})给出,那么其一点\boldsymbol x^\ast上的切平面定义为如下参数方程确定的曲面:
\boldsymbol x-\boldsymbol x _ 0=J\boldsymbol x(\boldsymbol t _ 0)\cdot\boldsymbol t.其中J\boldsymbol x表示\boldsymbol x(\boldsymbol t)的Jacobi矩阵。类似于x-x_0=vt+o(t)\, (t\to0)切线是x-x_0=vt。例如单位元\boldsymbol x=(\cos t,\sin t)的点\boldsymbol x _ 0=(\cos t _ 0,\sin t _ 0)上的切线/切平面可表示为
\begin{array}{c}{}\\\implies\\\implies\end{array}\begin{gathered}(x-\cos t _ 0,y-\sin t _ 0)=(-t\sin t _ 0,t\cos t _ 0),\\\sin t _ 0(y-\sin t _ 0)+\cos t _ 0(x-\cos t _ 0)=0,\\x _ 0x+y _ 0y=1.\end{gathered}这个定义给出的是参数方程的切平面,下面推导隐函数的切平面。
设曲面S:\boldsymbol h(\boldsymbol x)=\boldsymbol 0,\boldsymbol x^\ast是S上一点,假设\boldsymbol h在这点上满秩,也就是求导J\boldsymbol h(\boldsymbol x^\ast)行满秩,即\nabla h _ 1(\boldsymbol x^\ast),\dots,\nabla h _ m(\boldsymbol x^\ast)线性独立,此时称\boldsymbol x^\ast是一个正则点(regular point)、满足正则条件。如果\boldsymbol h是一个仿射函数,即\boldsymbol h(\boldsymbol x)=A\boldsymbol x+\boldsymbol b,那么正则条件即为A满秩,其判定与\boldsymbol x无关。
定理:对于曲面S:\boldsymbol h(\boldsymbol x)=\boldsymbol 0上的正则点\boldsymbol x^\ast,切平面等于
M=\{\boldsymbol d\mid J\boldsymbol h(\boldsymbol x^\ast)\boldsymbol d=\boldsymbol 0\}.说的是\nabla \boldsymbol h(\boldsymbol x^\ast)是切平面的法向量。
考虑其证明。设\boldsymbol x^1=(x _ 1,\dots,x _ {n-m}),\boldsymbol x^2=(x _ {n-m+1},\dots,x _ n),不妨设\boldsymbol h对\boldsymbol x^2求导是可逆的,\det J _ {\boldsymbol x^2}\boldsymbol h(\boldsymbol x^{\ast})\neq0,由连续性这一点在\boldsymbol x^\ast的附近也成立。利用隐函数定理,可解出\boldsymbol x^2=F(\boldsymbol x^1),于是得到参数表示\boldsymbol x=(\boldsymbol x^1,F(\boldsymbol x^1)),按定义切平面的参数方程是\boldsymbol x^1-\boldsymbol x _ \ast^1=I _ {n-m}\cdot(\boldsymbol x^1-\boldsymbol x^1 _ \ast)和\boldsymbol x^2-\boldsymbol x^2 _ \ast=JF(\boldsymbol x^1 _ \ast)(\boldsymbol x^1-\boldsymbol x^1 _ \ast)。第一条是平凡的,而第二条可利用JF(\boldsymbol x^1 _ \ast)=-(J _ {\boldsymbol x^2}\boldsymbol h(\boldsymbol x^\ast))^{-1}J _ {\boldsymbol x^1}\boldsymbol h(\boldsymbol x^\ast)化为
\begin{gathered}J _ {\boldsymbol x^1}\boldsymbol h(\boldsymbol x^\ast)(\boldsymbol x^1-\boldsymbol x^1 _ \ast)+J _ {\boldsymbol x^2}\boldsymbol h(\boldsymbol x^\ast)(\boldsymbol x^2-\boldsymbol x^2 _ \ast)=0,\\J\boldsymbol h(\boldsymbol x^\ast)(\boldsymbol x-\boldsymbol x^\ast)=0.\end{gathered}这表明切平面是与\boldsymbol h各个梯度都正交的向量组成的向量空间,即
M=\{\boldsymbol d\mid J\boldsymbol h(\boldsymbol x^\ast)\boldsymbol d=\boldsymbol 0\}.例如单位圆x^2+y^2=1,切线方程为(2x _ 0,2y _ 0)\cdot(x-x _ 0,y-y _ 0)=0,即x _ 0x+y _ 0y=1,和前面一致。
另一种常见做法是不从参数方程出发。设曲面S:\boldsymbol h(\boldsymbol x)=\boldsymbol 0,我们等价地定义在\boldsymbol x^\ast上其切平面为:S上过点\boldsymbol x^\ast的所有曲线的关于该点的切向量全体。定义的等价性此处不作证明了。
回到前面定理。记切平面为T,则T\subseteq M,因为只需要在\boldsymbol h(\boldsymbol x(t))=\boldsymbol 0两边对t求导并令t=0就得到J\boldsymbol h(\boldsymbol x^\ast)\boldsymbol x'(0)=\boldsymbol 0,故只需证M\subseteq T,即证对任何\boldsymbol d\in M,存在S上过点\boldsymbol x^\ast的曲线\boldsymbol x(t)使得\boldsymbol x'(0)=\boldsymbol d。
下面的构造略具技巧性,令\boldsymbol F(t,\boldsymbol u)=\boldsymbol h[\boldsymbol x^\ast+t\boldsymbol d+J\boldsymbol h(\boldsymbol x^\ast)^\mathsf T\boldsymbol u],其中\boldsymbol u\in\mathbb R^{m},要考虑方程\boldsymbol F(t,\boldsymbol u)=\boldsymbol 0。我们可以看到\boldsymbol F(0,\boldsymbol 0)=\boldsymbol 0;对\boldsymbol F关于\boldsymbol u求偏导,得J\boldsymbol h[\boldsymbol x^\ast+t\boldsymbol d+J\boldsymbol h(\boldsymbol x^\ast)^\mathsf T\boldsymbol u]J\boldsymbol h(\boldsymbol x^\ast)^\mathsf T,在(t,\boldsymbol u)=(0,\boldsymbol 0)有J _ {\boldsymbol u}\boldsymbol F(0,\boldsymbol 0)=J\boldsymbol h(\boldsymbol x^\ast)J\boldsymbol h(\boldsymbol x^\ast)^\mathsf T。
注意到正则条件已假设J\boldsymbol h(\boldsymbol x^\ast)行满秩,所以这个偏导是可逆的,由隐函数定理,存在t=0附近定义的连续可微\boldsymbol u(t)使得\boldsymbol F(t,\boldsymbol u(t))=\boldsymbol 0且\boldsymbol u(0)=\boldsymbol 0。现在就可以考察S上的曲线\boldsymbol x(t)=\boldsymbol x^\ast+t\boldsymbol d+J\boldsymbol h(\boldsymbol x^\ast)^\mathsf T\boldsymbol u(t),对\boldsymbol h(\boldsymbol x(t))=\boldsymbol 0两边对t求导并令t=0,得J\boldsymbol h(\boldsymbol x^\ast)[\boldsymbol y+J\boldsymbol h(\boldsymbol x^\ast)^\mathsf T\boldsymbol u'(0)]=\boldsymbol 0,由\boldsymbol d\in M可知\boldsymbol u'(0)=\boldsymbol 0,于是\boldsymbol x'(0)=\boldsymbol d+J\boldsymbol h(\boldsymbol x^\ast)^\mathsf T\boldsymbol u'(0)=\boldsymbol d,从而\boldsymbol d\in T。故T=M即证。
很多时候,T\subsetneqq M;T是不依赖曲面的表示的,而M则可能随\boldsymbol h的变动而变动。我们考虑h(x _ 1,x _ 2)=x _ 1,那么h(x _ 1,x _ 2)=0表示x _ 2轴,此时其上任意一点均正则;而若令h(x _ 1,x _ 2)=x _ 1^2,那么h(x _ 1,x _ 2)=0仍表示x _ 2轴:x _ 1=0,但Jh(0,x _ 2)=(2x _ 1,0)=\boldsymbol 0,故没有点满足正则条件,且此时M=\mathbb R^2。
一阶条件的准备工作
命题:设曲面S:\boldsymbol h(\boldsymbol x)=\boldsymbol 0,\boldsymbol x^\ast是S上f的极值点,且满足正则条件,那么对任何\boldsymbol d:
J\boldsymbol h(\boldsymbol x^\ast)\boldsymbol d=\boldsymbol 0\implies Jf(\boldsymbol x^\ast)\boldsymbol d=0.就是说极值点处切平面和f的梯度正交,或者换句话说,切平面包含于f等值线的切平面。例如约束x^2-y^2=1约束下的f=x^2+y^2极值,等值线是一系列同心圆,当双曲线切线和圆的切线不平行时,表明点附近可以取到更大更小的值,当到达平行时,f就达到极值了。
证明是简单的。设S上的曲线\boldsymbol x(t)满足\boldsymbol x(0)=\boldsymbol x^\ast,\boldsymbol x'(0)=\boldsymbol d,那么t=0是函数f(\boldsymbol x(t))的极值点,此即Jf(\boldsymbol x^\ast)\boldsymbol d=0。
接下来,我们断言:\nabla f(\boldsymbol x^\ast)可被\boldsymbol h在\boldsymbol x^\ast的梯度线性表示。
定理:设\boldsymbol x^\ast是在约束\boldsymbol h(\boldsymbol x)=\boldsymbol 0下f的极值点,且满足正则条件,那么存在\boldsymbol \lambda\in\mathbb R^m使得
\nabla f(\boldsymbol x^\ast)-\nabla \boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda=\boldsymbol 0.其中(\nabla\boldsymbol h)\boldsymbol \lambda=\lambda _ 1\nabla h _ 1+\dots+\lambda _ m\nabla h _ m。
考虑其证明。在线性规划的理论的基础上,证明是十分简单的。上面的命题表明,线性规划问题
\begin{aligned}\max &\quad \nabla f(\boldsymbol x^\ast)^\mathsf T\boldsymbol y,\\\text{s.t. }&\quad \nabla\boldsymbol h(\boldsymbol x^\ast)^\mathsf T\boldsymbol y=\boldsymbol 0\end{aligned}有最大值0,所以该问题的对偶问题可行,这表明此定理成立。
Lagrangian
如果用Lagrange乘数的语言来表述,引入Lagrange函数
L(\boldsymbol x,\boldsymbol \lambda)=f(\boldsymbol x)-\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x),这个一阶必要条件就是
\begin{gathered}
\nabla _ \boldsymbol x L(\boldsymbol x,\boldsymbol \lambda)=\boldsymbol 0,\\
\nabla _ \boldsymbol \lambda L(\boldsymbol x,\boldsymbol \lambda)=\boldsymbol 0.
\end{gathered}(第二个等式只是约束的等价表述)
Lagrange函数可以看作是目标函数加上一个惩罚违背约束的惩罚项,而诸\lambda _ i就是关于h _ i(\boldsymbol x)=0的惩罚权重了。取适当的\lambda _ i时,一个带约束的优化问题可被视作一个无约束的优化问题来解决。考虑特殊情况,当f是凸函数、\boldsymbol h是仿射函数A\boldsymbol x-\boldsymbol b,那么L(\boldsymbol x,\boldsymbol \lambda)也是关于\boldsymbol x的凸函数(对每个给定的\boldsymbol \lambda),因而若\boldsymbol x^\ast满足\nabla _ \boldsymbol x L=\boldsymbol 0,那么对同一个\boldsymbol \lambda它是不带约束地最小化L(\boldsymbol x,\boldsymbol \lambda)的最小值点;若进一步还有\boldsymbol h(\boldsymbol x^\ast)=\boldsymbol 0,那么\boldsymbol x^\ast也是带约束\boldsymbol h(\boldsymbol x)=\boldsymbol 0的最小化f(\boldsymbol x)的最小值点。
定理:对等式约束,一阶必要条件也是充分的,当f是凸函数且\boldsymbol h是仿射函数时。
二阶条件的准备工作
设f,\boldsymbol h\in C^2,则有
定理(必要条件):设\boldsymbol x^\ast是在约束\boldsymbol h(\boldsymbol x)=\boldsymbol 0下f的极小值点,且满足正则条件,那么存在\boldsymbol \lambda\in\mathbb R^m使得
\nabla f(\boldsymbol x^\ast)-\nabla \boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda=\boldsymbol 0,又设切平面M=\{\boldsymbol d\mid J\boldsymbol h(\boldsymbol x^\ast)\boldsymbol d=\boldsymbol 0\},那么在M上\nabla^2 f(\boldsymbol x^\ast)-\nabla^2\boldsymbol h(x^\ast)\boldsymbol \lambda半正定,其中(\nabla^2\boldsymbol h)\boldsymbol \lambda=\lambda _ 1\nabla^2 h _ 1+\dots+\lambda _ m\nabla^2 h _ m,简而言之,对任何\boldsymbol d\in M,
\boldsymbol d^\mathsf T\nabla^2 _ {\boldsymbol {xx}} L(\boldsymbol x^\ast,\boldsymbol \lambda)\,\boldsymbol d\geqslant0.
定理(充分条件):设\boldsymbol x^\ast,\boldsymbol \lambda满足\boldsymbol h(\boldsymbol x^\ast)=\boldsymbol 0,\nabla f(\boldsymbol x^\ast)-\nabla \boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda=\boldsymbol 0,矩阵\nabla^2 _ {\boldsymbol {xx}} L(\boldsymbol x^\ast,\boldsymbol \lambda)在M=\{\boldsymbol d\mid J\boldsymbol h(\boldsymbol x^\ast)\boldsymbol d=\boldsymbol 0\}上正定,即对任何M上的非零向量\boldsymbol d,
\boldsymbol d^\mathsf T\nabla^2 _ {\boldsymbol {xx}} L(\boldsymbol x^\ast,\boldsymbol \lambda)\boldsymbol d>0,那么,\boldsymbol x^\ast是满足\boldsymbol h(\boldsymbol x)=\boldsymbol 0约束的f的严格极小值点。
.
先证必要条件。考虑S:\boldsymbol h(\boldsymbol x)=\boldsymbol 0上过点\boldsymbol x^\ast的曲线\boldsymbol x=\boldsymbol x(t),满足\boldsymbol x(0)=\boldsymbol x^\ast,那么t=0是函数f(\boldsymbol x(t))的极小值点,二阶导在0必非负,一、二阶导分别为
\begin{gathered}Jf(\boldsymbol x(t))\boldsymbol x'(t),\\Jf(\boldsymbol x(t))\boldsymbol x''(t)+\boldsymbol x'(t)^\mathsf T\nabla^2 f(\boldsymbol x(t))\boldsymbol x'(t).\end{gathered}另一方面,对等式\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x(t))=0两边对t求两次导,得
\begin{gathered}\boldsymbol \lambda^\mathsf TJ\boldsymbol h(\boldsymbol x(t))\boldsymbol x'(t)=0,\\ \boldsymbol \lambda^\mathsf TJ\boldsymbol h(\boldsymbol x(t))\boldsymbol x''(t)+\boldsymbol x'(t)^\mathsf T[\nabla^2\boldsymbol h(\boldsymbol x(t))\boldsymbol \lambda]\boldsymbol x'(t)=0.\end{gathered}将此式取反加进f(\boldsymbol x(t))二阶导非负的式子,并利用一阶条件,得到\boldsymbol x'(0)^\mathsf T\nabla^2 _ {\boldsymbol x\boldsymbol x}\mathcal L(\boldsymbol x^\ast,\boldsymbol \lambda)\boldsymbol x'(0)\geqslant0,而\boldsymbol x'(0)可取M中的任何向量,故定理得证。
再证充分条件。由于\boldsymbol h(\boldsymbol x)=\boldsymbol 0约束下L=f,考虑证\boldsymbol x^\ast是L的严格极小值点。假设中已经知道\nabla L=\boldsymbol 0,故\boldsymbol x\to\boldsymbol x^\ast时
L(\boldsymbol x)-L(\boldsymbol x^\ast)=\frac12(\boldsymbol x-\boldsymbol x^\ast)^\mathsf T\nabla _ {xx}^2L(\boldsymbol x^\ast,\boldsymbol \lambda)(\boldsymbol x-\boldsymbol x^\ast)+o(\|\boldsymbol x-\boldsymbol x^\ast\|^2).设\boldsymbol h(\boldsymbol x)=\boldsymbol 0在\boldsymbol x^\ast的邻域有参数表示\boldsymbol x=\boldsymbol x(\boldsymbol t),满足\boldsymbol x(\boldsymbol 0)=\boldsymbol x^\ast。那么\boldsymbol x-\boldsymbol x^\ast=J\boldsymbol x(\boldsymbol 0)\cdot\boldsymbol t+\boldsymbol o(\boldsymbol t)(\boldsymbol t\to\boldsymbol 0),其中\boldsymbol d=J\boldsymbol x(\boldsymbol 0)\boldsymbol t是M上一个切向量。代入前式得到
L(\boldsymbol x(\boldsymbol t))-L(\boldsymbol x(\boldsymbol 0))=\frac12\boldsymbol d^\mathsf T\nabla _ {xx}^2L(\boldsymbol x^\ast,\boldsymbol \lambda)\boldsymbol d+o(\|\boldsymbol t\|).当\|\boldsymbol t\|充分小时上式为正,故\boldsymbol x^\ast是L的严格极小值点。
注记:二阶条件要求在切平面M上的正定性,而非整个空间,这就使得定理的应用没能那么直接,因为很可能发生整个空间上没有正定性但在切平面上有的情形。例如x^2+y^2-z^2在z=0约束下的最小值,最小值点的L二阶导可以算得是\operatorname{diag}(2,2,-2),它在整个空间不定,在切平面正定。
切平面是m个方程确定的n-m维平面,那么将m个变量用其余的表示出来即可。
例如求约束x^2/a^2+y^2/b^2=1下x^2+y^2的最值(设a>b>0),通过一阶必要条件得到四个点(\pm a,0),(0,\pm b),对应的\lambda分别是a^2,b^2。对Lagrange函数L=x^2+y^2-\lambda(x^2/a^2+y^2/b^2-1),\frac12\boldsymbol d^\mathsf T\nabla^2_{\boldsymbol {xx}} L(\boldsymbol x^\ast,\boldsymbol \lambda)\boldsymbol d=(1-\lambda/a^2)d_1^2+(1-\lambda/b^2)d_2^2。
求切线,(x_0,y_0)处切向量满足(2x _ 0/a^2,2y _ 0/b^2)\cdot(d_1,d_2)=0,令(x_0,y_0)=(\pm a, 0),得(d_1,d_2)=(0,d_2),代入前面,
\frac12\boldsymbol d^\mathsf T\nabla^2_{\boldsymbol {xx}} L(\boldsymbol x^\ast,\boldsymbol \lambda)\boldsymbol d=\Big(1-\frac\lambda{a^2}\Big)d_1^2+\Big(1-\frac\lambda{b^2}\Big)d_2^2=\Big(1-\frac{a^2}{b^2}\Big)d_2^2<0.在切线上负定,表明取极大值,也是最大值。同样可求得最小值。
一阶条件
现在回到问题
\begin{aligned}
\min &\quad f(\boldsymbol x)\\
\text{s.t. }&\quad \boldsymbol h(\boldsymbol x)=\boldsymbol 0,\;
\boldsymbol g(\boldsymbol x)\geqslant\boldsymbol 0,\\
&\quad \boldsymbol x\in\Omega.
\end{aligned}并设f,\boldsymbol g,\boldsymbol h\in C^1。
定义(LICQ):linear independence constraint qualification (LICQ) 是指,积极约束的梯度\{\nabla c _ i(\boldsymbol x),\, c _ i\in \mathcal A(\boldsymbol x)\}线性独立(其中\mathcal A代表积极约束的集合)。
现在可以再次给出KKT条件:
Karush-Kuhn-Tucker条件:令\boldsymbol x^\ast是上述带约束的优化问题的极小值点,且在该点LICQ (linear independence constraint qualification) 成立,那么存在m维向量\boldsymbol \lambda与p维非负向量\boldsymbol \mu\geqslant 0使得
\begin{gathered}\nabla f(\boldsymbol x^\ast)-\nabla \boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda-\nabla \boldsymbol g(\boldsymbol x^\ast)\boldsymbol \mu=\boldsymbol 0,\\\boldsymbol \mu^\mathsf T\boldsymbol g(\boldsymbol x^\ast)=0.\end{gathered}
第二条等式意味着\mu _ i非零仅当对应不等式约束是积极的,在线性规划中已经见过这种形式的关系了——complementary slackness,互补松弛条件。
考虑其证明。\boldsymbol x^\ast是约束集下的极小值点,那么将积极约束里的不等约束全部改为等式约束,也仍是极小值点。对于这些等式约束,\boldsymbol x^\ast是正则点,由前面的准备工作,存在Lagrange乘数,所以我们可知:第一条方程可以成立——对非积极约束我们可以令\mu _ i=0,这样第二条也跟着成立了。只剩下\boldsymbol \mu的非负性。
假设存在k,使得积极约束g _ k(\boldsymbol x^\ast)=0成立,但对应的\mu _ k<0。考虑约束\mathcal A\setminus\{g _ k\},对应曲面S'和切平面M',由于在\boldsymbol x^\ast有LICQ成立,\nabla g _ k不能被其余的积极约束的梯度线性表示。切平面M'中的向量是和其余梯度正交的向量集合,即M'是正交补,那么:切平面里应有向量\boldsymbol d使得\nabla g _ k(\boldsymbol x^\ast)^\mathsf T\boldsymbol d非零,否则\nabla g _ k(\boldsymbol x^\ast)和M'正交,必可被约束\mathcal A\setminus\{g _ k\}的梯度线性表示;由于M'是线性空间,可设\nabla g _ k(\boldsymbol x^\ast)^\mathsf T\boldsymbol d>0。
将\boldsymbol d和KKT条件里第一条等式作内积,\mathcal A\setminus\{g _ k\}的约束对应项都归零,得\nabla f(\boldsymbol x^\ast)^\mathsf T\boldsymbol d=\mu _ k\nabla g _ k(\boldsymbol x _ \ast)^\mathsf T\boldsymbol d<0——这意味着\boldsymbol d是f的下降方向,很容易构造矛盾。令\boldsymbol x(t)是S'上过点\boldsymbol x^\ast的曲线,满足\boldsymbol x(0)=\boldsymbol x^\ast,\boldsymbol x'(0)=\boldsymbol d,那么对充分小的t\geqslant0,\boldsymbol x(t)\in S,因为\boldsymbol x(t)\in S'且g _ k(\boldsymbol x(t))>0(因为\nabla g _ k(\boldsymbol x^\ast)^\mathsf T\boldsymbol d为正)。然而,对f(\boldsymbol x(t))关于t求导并令t=0,得\nabla f(\boldsymbol x^\ast)^\mathsf T\boldsymbol d,前面计算得负数,说明\boldsymbol x^\ast并非假设的极小值点。矛盾。
Lagrangian
同样可以引进Lagrange函数
L(\boldsymbol x,\boldsymbol \lambda,\boldsymbol \mu)=f(\boldsymbol x)-\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x)-\boldsymbol \mu^\mathsf T\boldsymbol g(\boldsymbol x).
同样地,Lagrange函数可以看作是无约束的目标函数,只是带上了两个惩罚违背约束的惩罚项。对于不等约束,若g _ i(\boldsymbol x)>0则不应有惩罚,\mu _ i=0,否则就应该是正值,使得要让目标函数最小化g _ i的值必须增大。
现在一阶必要条件可以表述为:
问题的原始约束(OVC) The Original Variable Constraints of Problem
Lagrange乘数的符号约束(MSC) The Multiplier Sign Constraints:\boldsymbol \lambda符号“自由”、\boldsymbol \mu\geqslant0(一般地,与\boldsymbol g同号)
Lagrangian导数条件(LDC) The Lagrangian Derivative Condition:
\nabla _ {\boldsymbol x}L(\boldsymbol x,\boldsymbol \lambda,\boldsymbol\mu )=\nabla f(\boldsymbol x)-\nabla\boldsymbol h(\boldsymbol x)\boldsymbol \lambda-\boldsymbol g(\boldsymbol x)\boldsymbol \mu=\boldsymbol 0.互补松弛条件(CSC) The Complementary Slackness Condition:\mu _ i g _ i(\boldsymbol x)=0,i=1,\dots,p。
考虑特殊情况,f,-\boldsymbol g是凸函数且\boldsymbol h是仿射函数:A\boldsymbol x-\boldsymbol b,那么对给定的\boldsymbol \lambda和非负\boldsymbol \mu\geqslant0,Lagrange函数对\boldsymbol x也是凸函数,对这组Lagrange乘数\boldsymbol x^\ast满足LDC,故是无约束优化L(\boldsymbol x,\boldsymbol \lambda,\boldsymbol \mu)的最小值点。
定理:若f,-\boldsymbol g分量都是凸函数且\boldsymbol h是仿射函数,一阶必要条件是充分的。
和前面只有等式约束相比需要些步骤来证明。
\begin{aligned}
0&\leqslant L(\boldsymbol x,\boldsymbol \lambda^\ast,\boldsymbol \mu^\ast)-\boldsymbol L(\boldsymbol x^\ast,\boldsymbol \lambda^\ast,\boldsymbol \mu^\ast)\\
&= f(\boldsymbol x)-f(\boldsymbol x^\ast)-\boldsymbol (\mu^\ast)^\mathsf T(\boldsymbol g(\boldsymbol x)-\boldsymbol g(\boldsymbol x^\ast))\\
&=f(\boldsymbol x)-f(\boldsymbol x^\ast)-\sum\nolimits _ {\mathcal A}\mu _ i(g _ i(\boldsymbol x)-g _ i(\boldsymbol x^\ast))\\
&=f(\boldsymbol x)-f(\boldsymbol x^\ast)-\sum\nolimits _ \mathcal A\mu _ ig _ i(\boldsymbol x)\\
&\leqslant f(\boldsymbol x)-f(\boldsymbol x^\ast).
\end{aligned}
二阶条件
二阶必要条件:设f,\boldsymbol g,\boldsymbol h\in C^2,\boldsymbol x^\ast是f的极小值点且满足LICQ,那么存在\boldsymbol \lambda和非负的\boldsymbol \mu\geqslant0使得KKT条件成立且
\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x^\ast,\boldsymbol \lambda,\boldsymbol\mu )=\nabla^2 f(\boldsymbol x^\ast)-\nabla^2\boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda-\nabla^2\boldsymbol g(\boldsymbol x^\ast)\boldsymbol \mu在\boldsymbol x^\ast的积极约束的切平面上是半正定的。
对于充分条件,只在切平面上作限定是不够的,因为可能有退化的(degenerate)不等约束(即积极约束的对应Lagrange乘数为零)。
二阶充分条件:设f,\boldsymbol g,\boldsymbol h\in C^2,下述条件是\boldsymbol x^\ast为f极小值点的充分条件:存在\boldsymbol \lambda和非负\boldsymbol \mu\geqslant0,\boldsymbol \mu^\mathsf T\boldsymbol g(\boldsymbol x^\ast)=0,\nabla f(\boldsymbol x^\ast)-\nabla \boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda-\nabla\boldsymbol g(\boldsymbol x^\ast)\boldsymbol \mu=\boldsymbol 0,且Hesse矩阵
\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x^\ast,\boldsymbol \lambda,\boldsymbol\mu )=\nabla^2 f(\boldsymbol x^\ast)-\nabla^2\boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda-\nabla^2\boldsymbol g(\boldsymbol x^\ast)\boldsymbol \mu在M'正定,这里M'为
\{\boldsymbol d\mid\nabla \boldsymbol h(\boldsymbol x^\ast)^\mathsf T\boldsymbol d=0,\, \nabla g _ i(\boldsymbol x^\ast)^\mathsf T\boldsymbol d=0,\, \forall i\in\{i\mid g _ i(\boldsymbol x^\ast)=0,\, \mu _ i>0\}\}.
可以看到,如果严格松弛互补条件(strict complementary slackness)成立,那么M'就是M(积极约束对应的切平面)。
必要条件是简单的,因为直接把积极约束全看做等式约束(正如开头所言)即可应用前面准备工作的结论。下证充分条件,反证之。若不成立,存在可行域上的\{\boldsymbol y _ k\}使得\boldsymbol y _ k\to \boldsymbol x^\ast但f(\boldsymbol y _ k)\leqslant f(\boldsymbol x^\ast)。设\boldsymbol \delta _ k=\boldsymbol y _ k-\boldsymbol x^\ast,\delta _ k=\|\boldsymbol y _ k-\boldsymbol x^\ast\|,那么\{(\boldsymbol y _ k-\boldsymbol x^\ast)\mathbin/\delta _ k\}作为有界点列存在收敛子列,不妨就设这个点列收敛到\boldsymbol s^\ast,则s _ k:=(\boldsymbol y _ k-\boldsymbol x^\ast)\mathbin/\delta _ k=\boldsymbol s^\ast+\boldsymbol r _ k,其中\boldsymbol r _ k\to\boldsymbol 0。
对f有0\geqslant f(\boldsymbol y _ k)-f(\boldsymbol x^\ast)=\delta _ k Jf(\boldsymbol x^\ast)\boldsymbol s _ k+o(\delta _ k),除\delta _ k并令k\to\infty得0\geqslant Jf(\boldsymbol x^\ast)\boldsymbol s^\ast;对\boldsymbol g(\boldsymbol x)\geqslant\boldsymbol 0中的积极约束,g _ i(\boldsymbol y _ k)-g _ i(\boldsymbol x^\ast)\geqslant0,同理可得Jg _ i(\boldsymbol x^\ast)\boldsymbol s^\ast\geqslant0;对\boldsymbol h则是Jh _ i(\boldsymbol x^\ast)\boldsymbol s^\ast=0。
如果\mu _ i>0对应的某个g _ i有Jg _ i(\boldsymbol x^\ast)\boldsymbol s^\ast>0,那么Jf(\boldsymbol x^\ast)\boldsymbol s^\ast=\boldsymbol \lambda^\mathsf TJ\boldsymbol h(\boldsymbol x^\ast)\boldsymbol s^\ast+\boldsymbol \mu^\mathsf T J\boldsymbol g(\boldsymbol x^\ast)\boldsymbol s^\ast>0,但是已经推出左边小于等于0,矛盾。如果积极约束都有Jg _ i(\boldsymbol x^\ast)\boldsymbol s^\ast=0,那么\boldsymbol s^\ast\in M'。将下面三式适当变换后相加
\begin{gathered}0\geqslant \delta _ k Jf(\boldsymbol x^\ast)\boldsymbol s _ k+\frac{\delta _ k^2}2\boldsymbol s _ k^\mathsf T\nabla ^2f(\boldsymbol \eta)\boldsymbol s _ k,\\0=\delta _ kJh _ j(\boldsymbol x^\ast)\boldsymbol s _ k+\frac{\delta _ k^2}2\boldsymbol s _ k^\mathsf T\nabla ^2h _ j(\boldsymbol \eta _ j^1)\boldsymbol s _ k,\\0=\delta _ kJg _ i(\boldsymbol x^\ast)\boldsymbol s _ k+\frac{\delta _ k^2}2\boldsymbol s _ k^\mathsf T\nabla ^2g _ i(\boldsymbol \eta _ i^2)\boldsymbol s _ k,\end{gathered}得到0\geqslant \frac{\delta_k^2}2\boldsymbol s_k^\mathsf T(\nabla^2f-\lambda_1\nabla^2h_1-\dots-\mu_1\nabla^2g_1-\dots)\boldsymbol s_k,令k\to\infty,则\boldsymbol s_k\to \boldsymbol s^\ast 以及诸 \boldsymbol \eta\to\boldsymbol x^\ast,得0\geqslant (\boldsymbol s^\ast)^\mathsf T\nabla^2_{xx}L(\boldsymbol x^\ast,\boldsymbol \lambda,\boldsymbol \mu)\boldsymbol s^\ast,由M'正定性右边大于0,矛盾。
对偶
Lagrange对偶
对偶理论在优化中非常重要。这里先初窥门径。为方便,先考虑不等约束的问题
\begin{aligned}
\min&\quad f(\boldsymbol x)\\
\text{s.t. }&\quad \boldsymbol g(\boldsymbol x)\geqslant0,\\
&\quad \boldsymbol x\in\Omega.
\end{aligned}这里\Omega只考虑凸集,f,\boldsymbol g当然在其上也要有定义。假设\boldsymbol g是p维的,且问题至少有一个可行点。定义一个primal函数
\omega(\boldsymbol z)=\inf\; \{f(\boldsymbol x)\mid \boldsymbol g(\boldsymbol x)\geqslant \boldsymbol z,\, \boldsymbol x\in \Omega\}.其定义域就是D=\{\boldsymbol z\mid \exist \boldsymbol x\in\Omega,\, \boldsymbol g(\boldsymbol x)\geqslant\boldsymbol z\}。这个函数图像与因变量坐标轴的交点就是目标函数的最值。对偶就是基于在primal函数图像之下的超平面的考虑而来。
不等约束的优化,对偶函数定义为\phi(\boldsymbol \mu)=\inf\; \{f(\boldsymbol x)-\boldsymbol \mu^\mathsf T\boldsymbol g(\boldsymbol x)\mid \boldsymbol x\in\Omega\}\, (\boldsymbol \mu\geqslant0),设所有使对偶函数有限的非负\boldsymbol \mu组成D,那么:
命题:在D上-\phi总是凸函数,由此D是凸集。
只需利用f(\boldsymbol x)-(\alpha\boldsymbol \mu _ 1+(1-\alpha)\boldsymbol \mu _ 2)^\mathsf T\boldsymbol g(\boldsymbol x)=\alpha f(\boldsymbol x)-\alpha\boldsymbol \mu _ 1^\mathsf T\boldsymbol g(\boldsymbol x)+(1-\alpha)f(\boldsymbol x)-(1-\alpha)\boldsymbol \mu _ 2^\mathsf T\boldsymbol g(\boldsymbol x),然后两边同时取下确界即可。
现在令\phi^\ast=\sup\phi(\boldsymbol \mu),又设f^\ast是原问题的目标函数最优值,那么有
命题(弱对偶):
\phi^\ast\leqslant f^\ast.
这是因为对\boldsymbol \mu\geqslant0有\phi(\boldsymbol \mu)\leqslant\inf\, \{f(\boldsymbol x)-\boldsymbol \mu^\mathsf T\boldsymbol g(\boldsymbol x)\mid \boldsymbol g(\boldsymbol x)\geqslant0,\, \boldsymbol x\in\Omega\}\leqslant\inf\, \{f(\boldsymbol x)\mid\boldsymbol g(\boldsymbol x)\geqslant0,\, \boldsymbol x\in\Omega\},再取上确界就得到该命题。
.
接下来关注对偶函数的几何含义。对\boldsymbol \mu\geqslant0,考虑向量(1,-\boldsymbol \mu)和常数c,它们能够定义一个超平面:(1,-\boldsymbol \mu)^\mathsf T(r,\boldsymbol z)=c,即r-\boldsymbol \mu^\mathsf T\boldsymbol z=c。当c取不同的值我们得到一系列平行的超平面。我们取c足够小,设存在点\boldsymbol x使r=f(\boldsymbol x),\boldsymbol z=\boldsymbol g(\boldsymbol x),那么此时最小的c=\phi(\boldsymbol \mu)。再设超平面与一个轴的交点(r _ 0,\boldsymbol 0),代进超平面方程得到c=r _ 0,就是说轴的截距给出了\phi(\boldsymbol \mu)。
考虑r-\boldsymbol z图,其中r=f(\boldsymbol x),\boldsymbol z=\boldsymbol g(\boldsymbol x),原问题最优解对应的是\boldsymbol z\geqslant0这半边的最低点(r^\ast,\boldsymbol z^\ast)。不难看出:这些(r,\boldsymbol z)点都在超平面r-\boldsymbol \mu^\mathsf T\boldsymbol z=\phi(\boldsymbol \mu)之上,这是\phi(\boldsymbol \mu)的定义决定的。而满足在这些点之下这一条件的超平面的截距不会超过r^\ast——这正是上面所说的弱对偶。原因也是一样,只考虑在\boldsymbol z\geqslant0这边的点之下的超平面的截距当然比考虑所有\boldsymbol z的要增大(因为只需要在更少的点下方),而正半边对应的最小截距当然是r^\ast(超平面r=r^\ast),所以总最小截距\phi(\boldsymbol \mu)要比r^\ast要小。
.
现在考虑包含等式约束的优化问题
\begin{aligned}
\min &\quad f(\boldsymbol x)\\
\text{s.t. }&\quad \boldsymbol h(\boldsymbol x)=\boldsymbol 0,\;
\boldsymbol g(\boldsymbol x)\geqslant\boldsymbol 0,\\
&\quad \boldsymbol x\in\Omega.
\end{aligned}\Omega仍是凸集。此时对偶函数定义为
\phi(\boldsymbol \lambda,\boldsymbol \mu)=\inf _ \boldsymbol x\; [f(\boldsymbol x)-\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x)-\boldsymbol \mu^\mathsf T\boldsymbol g(\boldsymbol x)],\quad \boldsymbol \mu\geqslant0.对偶问题则为
\phi^\ast=\sup _ {\boldsymbol \mu\geqslant0,\boldsymbol \lambda}\phi(\boldsymbol \lambda,\boldsymbol \mu).
弱对偶定理仍成立:\phi^\ast\leqslant f^\ast。
零阶充分条件:若\boldsymbol x与(\boldsymbol \lambda,\boldsymbol \mu)分别是原问题与对偶问题的可行解,使得f(\boldsymbol x)=\phi(\boldsymbol \lambda,\boldsymbol \mu),那么它们都分别是各自问题的全局最优解。
引入凸性的假设,可以有如下的强对偶定理:
强对偶定理:在上述原问题基础上,设f,-\boldsymbol g是凸函数,\boldsymbol h是仿射函数,设最小值为f(\boldsymbol x^\ast)=f^\ast,\boldsymbol x^\ast有LICQ(或Slater条件(SCQ)),且\boldsymbol x^\ast,\boldsymbol \lambda^\ast和非负\boldsymbol \mu^\ast\geqslant0满足KKT条件,那么
\phi^\ast=f^\ast.且\boldsymbol \lambda^\ast,\boldsymbol \mu^\ast是对偶问题的最优解。
此时Lagrange函数是凸函数,由零阶充分条件即证。
可以看到,KKT条件是充分的,在凸优化下还是必要的。
泛函分析中的对偶与优化中的对偶的联系
我们可以对优化中的对偶和泛函分析中的对偶作一点联系。但这里由于篇幅限制,且需要更深入的数学知识(泛函分析),已在 优化中的对偶与泛函分析中的对偶的联系 单独讨论。
简单来说,我们可以将分析放到更一般的框架中来,在一般的赋范线性空间中进行分析。此时弱对偶变成了共轭函数的性质f^{\ast\ast}\leqslant f;原问题是原空间上的优化问题,而对偶问题成为了一个在对偶空间上的优化问题;Lagrange函数中的Lagrange乘数即对应对偶空间中的向量。我们平时见到的是其特殊形式:考虑的空间是普通的欧氏空间,这样由Hilbert空间中的F. Riesz表示定理,其中的连续线性泛函可以与其中的向量一一对应,可以表示为它的内积形式,就得到了我们平时见到的常见形式。
局部对偶
上面的对偶理论是global的,下面简单过一些local的理论。
下面的分析对含不等约束的问题是完全类似的(只需要稍加改动),但为了叙述的简单只考虑等式约束:
\begin{aligned}
\min&\quad f(\boldsymbol x)\\
\text{s.t. }&\quad \boldsymbol h(\boldsymbol x)=\boldsymbol 0.
\end{aligned}这里的f,\boldsymbol h\in C^2。我们关注这个问题的一个局部解\boldsymbol x^\ast,假设这个局部解满足LICQ,那么,由一、二阶必要条件,存在Lagrange乘数\boldsymbol \lambda^\ast,使得\nabla f(\boldsymbol x^\ast)-\nabla\boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda^\ast=\boldsymbol 0,且\nabla^2 f(\boldsymbol x^\ast)-\nabla^2\boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda在切平面M=\{\boldsymbol d\mid J\boldsymbol h(\boldsymbol x^\ast)\boldsymbol d^\ast=\boldsymbol 0\}上半正定。
仍定义Lagrange函数为
L(\boldsymbol x,\boldsymbol \lambda)=f(\boldsymbol x)-\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x),那么\nabla _ \boldsymbol x L(\boldsymbol x^\ast,\boldsymbol \lambda^\ast)=\boldsymbol 0,且\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x^\ast,\boldsymbol \lambda^\ast)在M上半正定。
现在我们需要引入局部凸性的假设以给出局部对偶理论。具体来说,我们假设\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x^\ast,\boldsymbol \lambda^\ast)是正定矩阵;意即,第一,是严格正定而非半正定,第二,是在整个空间都是正定,而非仅在切平面M上。
在这个假设下,由一、二阶充分条件,\boldsymbol x^\ast是无约束优化问题\min _ {\boldsymbol x} L(\boldsymbol x,\boldsymbol \lambda^\ast)的一个局部解。
我们断言:对于\boldsymbol \lambda^\ast附近的\boldsymbol \lambda,存在\boldsymbol x^\ast附近的\boldsymbol x使L(\boldsymbol x,\boldsymbol \lambda)达到到极小值。首先,由于\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x^\ast,\boldsymbol \lambda^\ast)\succ 0,由隐函数定理,方程\nabla _ \boldsymbol x L(\boldsymbol x,\boldsymbol \lambda)=\boldsymbol 0对于\boldsymbol \lambda^\ast附近的\boldsymbol \lambda唯一确定了一个解\boldsymbol x,后面记作\boldsymbol x(\boldsymbol \lambda);由连续性假设,\boldsymbol \lambda充分接近\boldsymbol \lambda^\ast时,\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x,\boldsymbol \lambda)\succ0——所以,在局部范围内有一个连续可微的\boldsymbol \lambda,\boldsymbol x间的对应关系,这个关系通过它们是无约束优化问题的解,即极小化Lagrange函数,来体现。
我们在\boldsymbol \lambda^\ast附近定义一个对偶函数\phi:
\phi(\boldsymbol \lambda)=\min _ {\boldsymbol x\in N(\boldsymbol x^\ast)}L(\boldsymbol x,\boldsymbol \lambda)=\min _ {\boldsymbol x\in N(\boldsymbol x^\ast)}[f(\boldsymbol x)-\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x)].这里的最小是在局部范围内——\boldsymbol x^\ast的邻域N(\boldsymbol x^\ast)。下面可以看到局部上带约束的原问题等价于对偶函数\phi关于\boldsymbol \lambda的无约束的局部极大化。因而我们建立了带约束优化问题中的\boldsymbol x和无约束优化问题中的\boldsymbol \lambda的一种联系。
命题:对偶函数的梯度有简单的形式
\nabla\phi(\boldsymbol \lambda)=-\boldsymbol h(\boldsymbol x(\boldsymbol \lambda)).命题:对偶函数的Hesse矩阵为
\nabla^2\phi(\boldsymbol \lambda)=-\nabla\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))^\mathsf T[\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x(\boldsymbol \lambda),\boldsymbol \lambda)]^{-1}\nabla\boldsymbol h(\boldsymbol x(\boldsymbol \lambda)).
证明:首先梯度可以通过直接计算得到,\phi(\boldsymbol \lambda)=f(\boldsymbol x(\boldsymbol \lambda))-\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x(\boldsymbol \lambda)),求导得
\begin{aligned}
J\phi(\boldsymbol \lambda)&=Jf(\boldsymbol x(\boldsymbol \lambda))J\boldsymbol x(\lambda)-\boldsymbol \lambda^\mathsf TJ\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))J\boldsymbol x(\boldsymbol \lambda)-\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))^\mathsf T\\
\nabla\phi(\boldsymbol \lambda)&=\nabla\boldsymbol x(\boldsymbol \lambda)[\nabla f(\boldsymbol x(\boldsymbol \lambda))-\nabla \boldsymbol h(\boldsymbol x(\boldsymbol \lambda))\boldsymbol \lambda]-\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))\\
&=-\boldsymbol h(\boldsymbol x(\boldsymbol \lambda)).
\end{aligned}由此亦知Hessian为-\nabla \boldsymbol x(\boldsymbol \lambda)\nabla\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))。对\nabla f(\boldsymbol x(\boldsymbol \lambda))-\nabla \boldsymbol h(\boldsymbol x(\boldsymbol \lambda))\boldsymbol \lambda=\boldsymbol 0关于\boldsymbol \lambda求导,得
\begin{aligned}
\boldsymbol 0&=Hf(\boldsymbol x(\boldsymbol \lambda))J\boldsymbol x(\boldsymbol \lambda)-\boldsymbol \lambda^\mathsf TH\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))J\boldsymbol x(\boldsymbol \lambda)-\nabla\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))
\\
\nabla\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))^\mathsf T&=\nabla\boldsymbol x(\boldsymbol \lambda)[\nabla^2f(\boldsymbol x(\boldsymbol \lambda))-\nabla^2\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))\boldsymbol \lambda]\\
&=\nabla\boldsymbol x(\boldsymbol \lambda)\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x(\boldsymbol \lambda),\boldsymbol \lambda)\\
\nabla\boldsymbol x(\boldsymbol \lambda)&=\nabla\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))^\mathsf T[\nabla^2 _ {\boldsymbol {xx}}L(\boldsymbol x(\boldsymbol \lambda),\boldsymbol \lambda)]^{-1},
\end{aligned}代入Hessian即证。
.
观察\phi的Hesse矩阵,我们可以推断这是个负定矩阵。于是,有
定理(局部对偶):(在前文的设置下)又设原问题在\boldsymbol x^\ast处的极小值为r^\ast,则对偶问题\max\phi(\boldsymbol \lambda)有局部最优解\boldsymbol \lambda^\ast且极大值也为r^\ast。
前面已求出\phi的梯度,于是我们可以有如下的dual ascent(对偶上升法):
dual ascent:迭代过程为
\begin{aligned}
\boldsymbol x _ {k+1}&=\operatorname*{\arg\min}\nolimits _ {\boldsymbol x}L(\boldsymbol x,\boldsymbol \lambda _ k,\boldsymbol \mu _ k),\\
\boldsymbol \lambda _ {k+1}&=\boldsymbol \lambda _ k-\rho _ k\boldsymbol h(\boldsymbol x _ {k+1}),\\
\boldsymbol \mu _ {k+1}&=\max\{\boldsymbol 0,\, \boldsymbol \mu _ k-\rho _ k\boldsymbol g(\boldsymbol x _ {k+1})\}.
\end{aligned}这一方法的具体分析,可参考更深入的文献。
Augmented Lagrangian,ADMM
Augmented Lagrangian
dual ascent要求的条件比较强。可被改进为Augmented Lagrangian method,亦称作是method of multipliers。
对于等式约束\boldsymbol h(\boldsymbol x)=\boldsymbol 0的优化问题\min f(\boldsymbol x),其augmented Lagrangian为
L _ \rho(\boldsymbol x,\boldsymbol \lambda)=f(\boldsymbol x)-\boldsymbol \lambda^\mathsf T\boldsymbol h(\boldsymbol x)+\frac{\rho}{2}|\boldsymbol h(\boldsymbol x)|^2.这里的\rho>0称作是惩罚参数(为零时就是标准的Lagrange函数)。这个函数也可以看作是问题
\begin{aligned}
\min&\quad f(\boldsymbol x)+\frac\rho2|\boldsymbol h(\boldsymbol x)|^2\\
\text{s.t. }&\quad \boldsymbol h(\boldsymbol x)=\boldsymbol 0
\end{aligned}的Lagrange函数,而这个问题显然和原问题等价。此时再应用dual ascent,得到迭代过程
\begin{aligned}
\boldsymbol x _ {k+1}&=\operatorname*{\arg\min}\nolimits _ {\boldsymbol x} L _ \rho(\boldsymbol x,\boldsymbol \lambda _ k),\\
\boldsymbol \lambda _ {k+1}&=\boldsymbol \lambda _ k-\rho\boldsymbol h(\boldsymbol x _ {k+1}).
\end{aligned}这里的\rho使用了常数的设置,当然也可以用变化的设置,例如趋向于某一常数,再如以某一速度趋于无穷。
分析
这个过程看起来和原来的dual ascent没什么区别,然而原来的dual ascent对局部的凸性作了假设,当局部凸性不成立时就不好应用了。此时augmented Lagrangian里的\frac\rho2|\boldsymbol h(\boldsymbol x)|^2一项就起到了将局部“凸化”的作用。对于大\rho,Lagrangian确实变成了局部凸的,因而对偶方法可以应用。
命题:设\boldsymbol x^\ast,\boldsymbol \lambda^\ast满足二阶充分条件使得f被极小化,那么存在\rho^\ast使\rho>\rho^\ast时,L _ \rho(\boldsymbol x,\boldsymbol \lambda^\ast)都在\boldsymbol x^\ast处取得极小。
考虑证明。求Hesse矩阵得\nabla^2 _ {\boldsymbol {xx}}L _ \rho(\boldsymbol x^\ast,\boldsymbol \lambda^\ast)=\nabla^2 f(\boldsymbol x^\ast)-\nabla^2\boldsymbol h(\boldsymbol x^\ast)\boldsymbol \lambda^\ast+\rho \nabla \boldsymbol h(\boldsymbol x^\ast)\nabla \boldsymbol h(\boldsymbol x^\ast)^\mathsf T,第一第二项即原始Hessian,由于满足二阶充分条件,在切平面\{\boldsymbol d\mid \nabla\boldsymbol h(\boldsymbol x)^\mathsf T\boldsymbol d=\boldsymbol 0\}上是正定的;而最后一项是半正定的。若命题不成立,则存在一列单位向量\{\boldsymbol d _ k\} _ {k=1}^\infty使得\boldsymbol d _ k^\mathsf T(A+c _ kB)\boldsymbol d _ k\leqslant0,其中A表示原始Hessian,B表示\nabla\boldsymbol h\nabla\boldsymbol h^\mathsf T,c _ k是一列趋于正无穷的数。\{\boldsymbol d _ k\}有界则存在收敛子列,不妨设\boldsymbol d _ k\to\boldsymbol d,那么应有\boldsymbol d^\mathsf TB\boldsymbol d=0,于是\boldsymbol d^\mathsf TA\boldsymbol d\leqslant0,但是前一式意味着B\boldsymbol d=\boldsymbol 0,就与命题假设矛盾。最后再次用二阶充分条件即证。
命题:\rho充分大时,对\boldsymbol \lambda^\ast附近的\boldsymbol \lambda,L _ \rho(\boldsymbol x,\boldsymbol \lambda)在\boldsymbol x^\ast附近有唯一极小值点\boldsymbol x。
这个和L(\boldsymbol x,\boldsymbol \lambda)时的分析是一样的,证明不再赘述。
现在,如果\boldsymbol \lambda使得\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))=\boldsymbol 0,那么由于此时这组\boldsymbol x,\boldsymbol \lambda满足问题\min\, \{f(\boldsymbol x)+\frac\rho2|\boldsymbol h(\boldsymbol x)|^2\mid\boldsymbol h(\boldsymbol x)=\boldsymbol 0\}的充分条件,它们必为\boldsymbol x^\ast,\boldsymbol \lambda^\ast,所以\boldsymbol \lambda的选定可视作解\boldsymbol h(\boldsymbol x(\boldsymbol \lambda))=\boldsymbol 0。解这个方程的一种迭代就是\boldsymbol \lambda _ {k+1}=\boldsymbol \lambda _ k-\rho\boldsymbol h(\boldsymbol x(\boldsymbol \lambda _ k)),它会在\boldsymbol \lambda^\ast的邻域以线性的速度收敛。
几何解释
考虑primal函数\omega(\boldsymbol y)=\min\, \{f(\boldsymbol x)\mid \boldsymbol h(\boldsymbol x)=\boldsymbol y,\, \boldsymbol x\in N(\boldsymbol x^\ast)\},可以证明\omega(\boldsymbol 0)=f(\boldsymbol x^\ast)及\nabla\omega(\boldsymbol 0)=\boldsymbol \lambda^\ast,细节略过,只给出大意:设\boldsymbol h(\boldsymbol x)=\boldsymbol y下极小值点为\boldsymbol x(\boldsymbol y),对\boldsymbol y=\boldsymbol h(\boldsymbol x(\boldsymbol y))关于\boldsymbol y求导并令\boldsymbol y=\boldsymbol 0,I=J\boldsymbol h(\boldsymbol x^\ast)J\boldsymbol x(\boldsymbol 0),从而J\omega(\boldsymbol 0)=J _ \boldsymbol y(f(\boldsymbol x(\boldsymbol y)))| _ {\boldsymbol y=\boldsymbol 0}=Jf(\boldsymbol x^\ast)J\boldsymbol x(\boldsymbol 0)=(\boldsymbol \lambda^{\ast})^\mathsf TJ\boldsymbol h(\boldsymbol x^\ast)J\boldsymbol x(\boldsymbol 0)=(\boldsymbol \lambda^\ast)^\mathsf T,即证。
用这个primal函数,
\begin{aligned}
\min L _ \rho(\boldsymbol x,\boldsymbol \lambda _ k)&=\min _ \boldsymbol x\, \big[f(\boldsymbol x)-\boldsymbol \lambda _ k^\mathsf T\boldsymbol h(\boldsymbol x)+\frac\rho2|\boldsymbol h(\boldsymbol x)|^2\big]\\
&=\min _ {\boldsymbol {x,y}}\, \big\{f(\boldsymbol x)-\boldsymbol \lambda _ k^\mathsf T\boldsymbol y+\frac\rho2|\boldsymbol y|^2\mid \boldsymbol h(\boldsymbol x)=\boldsymbol y\big\}\\
&=\min _ \boldsymbol y\, \big[\omega(\boldsymbol y)-\boldsymbol \lambda^\mathsf T _ k\boldsymbol y+\frac\rho2|\boldsymbol y|^2 \big]
.
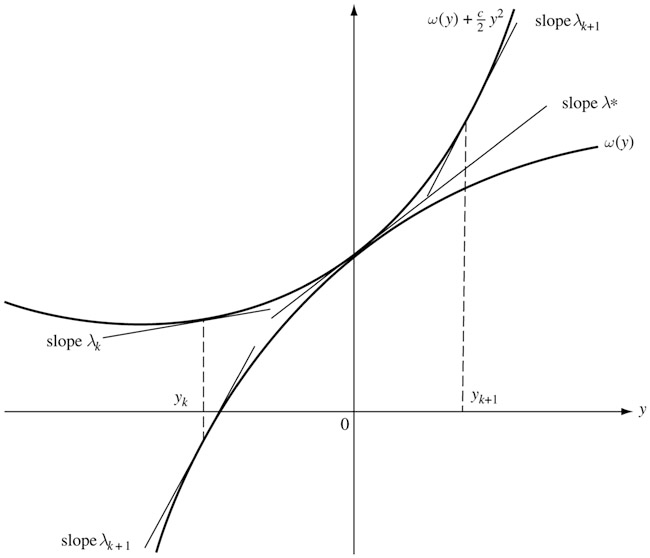
\end{aligned}这里面对\boldsymbol y的最小是在\boldsymbol 0的邻域内取的。对于单约束,下图展示了这一最小化的过程。有了\lambda _ k后y _ k应满足\omega(y)+\frac\rho2y^2在它上面切线斜率恰为\lambda _ k,然后\omega(y)在y _ k的斜率正是\lambda _ {k+1}。这是因为\boldsymbol y _ k既然使\omega(\boldsymbol y)-\boldsymbol \lambda^\mathsf T _ k\boldsymbol y+\frac\rho2|\boldsymbol y|^2最小,那么\nabla\omega(\boldsymbol y _ k)+\rho\boldsymbol y _ k=\boldsymbol \lambda _ k,故\boldsymbol \lambda _ {k+1}=\boldsymbol \lambda _ k-\rho\boldsymbol h(\boldsymbol x(\boldsymbol \lambda _ k))=\boldsymbol \lambda _ k-\rho\boldsymbol y _ k=\nabla\omega(\boldsymbol y _ k)。
The Alternating Direction Method of Multipliers
这一节推荐查阅著名文献:
S. Boyd and N. Parikh and E. Chu and B. Peleato and J. Eckstein (2010), “Distributed optimization and statistical learning via the alternating direction method of multipliers”
.
虽然augmented Lagrangian有更好的收敛,但是会失去问题的decomposability。(Separability is ruined by augmented Lagrangian ...)
ADMM算法试图结合dual ascent和augmented Lagrangian的优点。(ADMM is an algorithm that is intended to blend the decomposability of dual ascent with the superior convergence properties of the method of multipliers.)
考虑问题
\begin{aligned}
\min&\quad f(\boldsymbol x)+g(\boldsymbol y)\\
\text{s.t. }&\quad A\boldsymbol x+B\boldsymbol y=\boldsymbol b.
\end{aligned}最优值设为p^\ast,augmented Lagrangian写为
L _ \rho(\boldsymbol x,\boldsymbol y,\boldsymbol \lambda)=f(\boldsymbol x)+g(\boldsymbol y)-\boldsymbol \lambda^\mathsf T(A\boldsymbol x+B\boldsymbol y-\boldsymbol b)+\frac\rho2|A\boldsymbol x+B\boldsymbol y-\boldsymbol b|^2,可以看到惩罚项会有\boldsymbol x,\boldsymbol y的耦合,而ADMM则交替分而治之,是谓alternating direction,迭代步骤为:
\begin{aligned}
\boldsymbol x _ {k+1}&=\operatorname*{\arg\min}\nolimits _ \boldsymbol x L _ \rho(\boldsymbol x,\boldsymbol y _ k,\boldsymbol \lambda _ k),\\
\boldsymbol y _ {k+1}&=\operatorname*{\arg\min}\nolimits _ \boldsymbol y L _ \rho(\boldsymbol x _ {k+1},\boldsymbol y,\boldsymbol \lambda _ k),\\
\boldsymbol \lambda _ {k+1}&=\boldsymbol \lambda _ k-\rho(A\boldsymbol x _ {k+1}+B\boldsymbol y _ {k+1}-\boldsymbol b).
\end{aligned}
对于ADMM的收敛,这里只给出如下定理:
定理:设f,g是闭的凸函数,unaugmented Lagrangian有一个鞍点,即存在(\boldsymbol x^\ast,\boldsymbol y^\ast,\boldsymbol \lambda^\ast)使得
L _ 0(\boldsymbol x^\ast,\boldsymbol y^\ast,\boldsymbol \lambda)\leqslant L _ 0(\boldsymbol x^\ast,\boldsymbol y^\ast,\boldsymbol \lambda^\ast)\leqslant L _ 0(\boldsymbol x,\boldsymbol y,\boldsymbol \lambda^\ast),那么ADMM满足:
- 残差收敛:A\boldsymbol x _ k+B\boldsymbol y _ k-\boldsymbol b\to\boldsymbol 0,即迭代逐渐达到feasibility;
- 目标函数收敛:f(\boldsymbol x _ k)+g(\boldsymbol y _ k)\to p^\ast,即迭代逐渐达到最优;
- 对偶变量收敛:\boldsymbol \lambda _ k\to\boldsymbol \lambda^\ast,其中\boldsymbol \lambda^\ast为使得\inf _ {\boldsymbol x,\boldsymbol y}L _ 0(\boldsymbol x,\boldsymbol y,\boldsymbol \lambda)最小的点。
注意\boldsymbol x _ k,\boldsymbol z _ k不必收敛到最优。

发表回复