导引
一般来说,强化学习 (Reinforcement learning) 被认为是机器学习的一个分支。但其“风格”和通常所见的机器学习,无论是监督学习还是无监督学习,有着非常明显的差异,因此强化学习有它的相对“独立性”,在讨论机器学习的时候通常会见到把它“省略”的情况。尽管如此,强化学习的重要性还是不可忽视的,尤其是在人工智能中。
强化学习通常关注的是一个智能体agent在一个动态的环境中的学习。可以看到,和一般的机器学习相比,RL强调了环境的作用,agent通过与环境的互动获取经验,从而变得更为“智能”。在这个过程中,选择不同的“互动方式”,会学习到不同的经验,因为环境会作出不同的回应。而且学习与互动是一起进行的,有一个“行动→反馈→行动→……”的过程;但在监督或无监督学习里,模型一般是一下子收集完数据后训练得到的。同时还可以看到,“时间”在这里也有着一席之地,例如agent有时需要关注更长期的未来收益。如此看来,强化学习与其它机器学习确实有不小的差异。
如何“强化学习”?这就是本文所想讨论的主要内容。本文的结构包括了一些强化学习主体的基础、进阶和前沿。
- 第一部分梳理了经典RL的内容,包括了强化学习基础要素、dynamic programming、model-free evaluation/optimization等小节。
- 第二部分梳理了近似方法、policy gradient方法,可以用于大规模问题的解决。
- 第三部分包括了模仿学习、RLHF、offline RL、MCTS与AlphaGo等小节。
Contents
强化学习基础要素
基本建模
在时间上,RL通常考虑离散化的序列化时间。在每一时间步t都会有一个标量的回报reward r _ t来反映agent行动的好坏。Agent的目标则是最大化累积回报。强化学习假设我们总可以把目标建模成这个标量。
在每一步时间t上,agent采取行动action a _ t,然后环境作出回应,得到观测observation o _ t和回报reward r _ t,agent接收到它们后可以在下一个时间步做出新的行动,做出新的行动依据的是之前的历史history \boldsymbol h _ t=(a _ 1,o _ 1,r _ 1,\dots, a _ t,o _ t,r _ t)。一般地,我们会从历史中提取出所有对未来有用的信息,作为状态state,这样就定义了一个历史的函数:s _ t=f(\boldsymbol h _ t)。这样,在每一步要选择action我们只需要知道s _ t即可,过去的s _ 1,\dots,s _ {t-1}就可以舍弃掉了。
在环境上,一般地,基本的建模是一个Markov决策过程,即 MDP (Markov decision process) 。包含了:
- State的集合:\mathcal S;
- Action的集合:\mathcal A;
- 转移概率:P(s _ {t+1}|s _ t,a _ t);
- (即时的)reward函数分布(或联合分布)r _ t\sim p(r _ t)(或r _ t,s _ {t+1}\sim p(r _ t,s _ {t+1}))。
Agent的策略policy确定了其如何根据当前state来选择action,用\pi表示。这个策略policy可以是确定性的,是一个函数\pi:\mathcal S\to\mathcal A;也可以是随机性的,这样\pi(a|s)=P(a _ t=a\mid s _ t=s)。
在这些建模基础上,agent进行强化学习。在学习过程中,一般来说我们需要prediction(或者说evaluation)和control(或者说optimization)。前者评估一个policy会得到多少reward,后者用于寻找最优policy。
Value函数
通常,还会引入一个Horizon H(可无限)及一个因子\gamma,然后考虑Return G _ t=r _ t+\gamma r _ {t+1}+\dots+\gamma^{H-1}r _ {t+H-1}。下面我们都令H=\infty,这样为了避免无穷return,因子\gamma选择小于1,表示相同的reward,每过一个时间步,收益就要打个折扣,也是比较自然的。在此基础上,可以定义State Value Function V(s):
V(s)=E _ {\pi}[G _ t|s]=E _ {\pi}[r _ t+\gamma r _ {t+1}+\dots+\gamma^{H-1}r _ {t+H-1}\mid s _ t=s].
本文用R _ t表示r _ t的期望,即R _ t=E[r _ t],这样R(s,a)表示E[r|s,a],等等。
对无限horizon,可以写
\begin{aligned}
V(s)&=R(s)+\gamma\cdot E[r _ {t+1}+\dots+\gamma^{H-2}r _ {t+H-1}+\dots\mid s _ t=s]\\
&=R(s)+\gamma\cdot\sum _ {s'\in\mathcal S}P(s'|s)V(s').
\end{aligned}如果是有限MDP,将所有V的值写在一个向量里,就是\boldsymbol V=\boldsymbol R+\gamma P\boldsymbol V,其中P是转移概率矩阵。从中可以(理论上)显式地解出这个向量:\boldsymbol V=(I-\gamma P)^{-1}\boldsymbol R,也可以迭代求解:V(s)\leftarrow R(s)+\gamma\sum _ {s'}P(s'|s)V(s')。当然,上述V函数没有涉及到行动action。在policy \pi下,R(s)应为\sum _ {a}\pi(a|s)R(s,a),P(s'|s)则应为\sum _ {a}\pi(a|s)P(s'|s,a)。Policy evaluation的迭代式写为了
V(s)\leftarrow \sum _ {a\in\mathcal A}\pi(a|s)\Big[R(s,a)+\gamma\sum _ {s'\in\mathcal S}P(s'|s,a)V(s')\Big].
除了V函数,还有一个重要的Q函数,State-Action Value Function Q(s,a):
Q(s,a)=R(s,a)+\gamma\sum _ {s'\in\mathcal S}P(s'|s,a)V(s').
其对a\sim\pi(a|s)求期望正是V函数。可用于Policy improvement:\pi(s)\leftarrow\operatorname{\arg\max} _ a Q(s,a)。
附:
在下一节之前,对Markov链的一些特殊性质做一些简要回顾。以下只讨论离散的情况。
Irreducibility:任意两个state x,y都满足:从x出发有非0的概率能够到达y。
Recurrence&Transience:如果从x出发有非零的概率永远无法返回x,那么x称作是transient的,反之以概率1能够返回x,那么称作是recurrent的。如果从一个recurrent的x出发,离开x的情况下期望回到x的时间是有限的,那么x称作是positive recurrent的;反之若需要无限的时间,则称作是null recurrent的。
例:一个非常具体的例子。考虑一个定义在\mathbb N上的Markov链,x>0时P(x\to x+1)=p,P(x\to x-1)=q:=1-p,而x=0时以概率1转移到1。直观上,p>1/2时x倾向于向右移动,很可能是transient,p<1/2时x倾向于向左移动,很可能是recurrent,p=1/2时左右摇摆;可以计算它的recurrence/transience。当p>1/2时,可以证明此时Markov链transient。只需考虑1是transient的(该Markov链irreducible,因此recurrence/transience变为整体性质),以p _ i记从i出发后能够在某步到达1的概率,有递推式p _ i=pp _ {i+1}+qp _ {i-1}\, (i>0),同时由定义p _ 0=1。\{p _ i\}对应的特征方程为px^2-x+q=(x-1)(px-q)=0,根为x _ 1=1,x _ 2=q/p。当p\neq1/2时x _ 1\neq x _ 2,有表示p _ i=A(q/p)^i+B,由p _ 0=1可知可进一步写为p _ i=A(q/p)^i+1-A,可以推知A置为1,于是p _ i=(q/p)^i,p _ 1=q/p\in(0,1),这表明1是transient的。当0<p<1/2时,为使p _ i\in[0,1]必须A=0,于是p _ i=1,这表明此时是recurrent的。当p=1/2,p _ i=B+Ai,令i=0知B=1,为使p _ i\in[0,1]必须A=0,于是此时也是recurrent的。Positive recurrent和null recurrent的区分也是差不多的,同样只需要考虑1。设从i出发首次到1的期望时间是n _ i,那么有n _ 0=1,n _ 1=0,n _ i=1+pn _ {i+1}+qn _ {i-1}\, (n>1)。若p=1/2,那么n _ i=-i^2+B+Ai \, (i\geqslant 1),但i充分大时会变负数,于是只能n _ i=\infty \, (i>1),从而1必null recurrent。当p\in(0,1/2),n _ i=\frac{i}{q-p}+A(q/p)^i+B\, (i\geqslant 1),我们可以从中得知n _ i=\frac{i-1}{q-p},这表明从2出发期望回到1的时间是有限的,而另一方面从0出发回到1的时间也是有限的,所以从1出发离开1再回到1的期望时间是有限的,于是此时positive recurrent。
平稳分布 (Invariant distribution / stationary distribution):如果一个分布\mu满足对所有states y都有\sum _ x P(y|x)\mu(x)=\mu(y),那么这个分布称作是平稳分布。定义表明,如果初始的分布是平稳分布,那么后续也会是一样的分布。对平稳分布有如下结果(证明可参看其它资料):
定理:如果任一state是transient的,那么平稳分布不存在。
定理:如果Markov链positive recurrent,那么平稳分布存在。
定理:Irreducible的Markov链至多只存在一个平稳分布。
定理:令Markov链X irreducible。那么,X是positive recurrent的充要条件是平稳分布存在。在这情况下平稳分布唯一且\mu(x)=1\mathbin/E _ x\big[\, \inf\{n{\geqslant}1| x _ n{=}x\}\, \big]。(E _ x表示计算的是从x出发的期望)
考虑Markov链的收敛,我们引入aperiodic的性质。
Aperiodicity:若所有使得从x回到x概率非零的“时间”满足:它们最大公约数非1,那么x是periodic的;如果所有x周期都是1,那么这个Markov链是aperiodic的。例如时钟上的12个数,从1回到1最大公约数是12,其它数也是如此,12就是周期。
定理(Markov链的收敛):令X为一个irreducible、positive recurrent的Markov链,平稳分布为\pi。设从x出发,那么X为aperiodic,当且仅当X _ n的分布收敛到平稳分布:
\|\mathcal L _ x(X _ n)-\pi\| _ {\mathrm{TV}}\to 0,\quad n\to\infty.这里\|\cdot\| _ {\mathrm{TV}}表示total variation norm。
Dynamic programming
当我们对环境完全已知,即对MDP完全已知时,就可以用dynamic programming的算法。因为要求对环境已知,而且计算开销也不小,因而DP更多在于理论上的意义。
Policy iteration
在前面的policy evaluation和policy improvement的基础上,我们得到MDP的policy iteration (PI):
令i=0并初始化\pi _ 0
当policy未收敛时执行以下循环:
对每一s:
Policy evaluation:V(s)\leftarrow \sum _ {a\in\mathcal A}\pi _ i(a|s)\Big[R(s,a)+\gamma\sum _ {s'\in\mathcal S}P(s'|s,a)V _ {\pi _ i}(s')\Big]
Policy improvement:\pi _ {i+1}(s)\leftarrow\operatorname{\arg\max} _ a Q _ {\pi _ i}(s,a)
i\leftarrow i+1
这个算法每一步得到一个确定性policy,是能使V函数单调增的。这是因为对任一s,
\begin{aligned}
V _ {\pi _ i}(s)&\leqslant Q _ {\pi _ i}(s,\pi _ {i+1}(s))=R(s,\pi _ {i+1}(s))+\gamma\cdot E _ {s'}[V _ {\pi _ i}(s')|s,\pi _ {i+1}(s)]\\
&\leqslant R(s,\pi _ {i+1}(s))+\gamma\cdot E _ {s'}[Q _ {\pi _ i}(s',\pi _ {i+1}(s'))|s,\pi _ {i+1}(s)]\\
&=R(s,\pi _ {i+1}(s))+\gamma\cdot E _ {s'}\Big[R(s',\pi _ {i+1}(s'))+\gamma\cdot E _ {s''}[V _ {\pi _ i}(s'')|s',\pi _ {i+1}(s')]\Big|s,\pi _ {i+1}(s)\Big]\\
&\leqslant\cdots\\
&=E _ {\pi _ {i+1}}[R _ t+\gamma R _ {t+1}+\gamma^2 R _ {t+2}+\dots|s]\\
&=V _ {\pi _ {i+1}}(s).
\end{aligned}有限MDP中,policy有限而V函数单调,那么最后就肯定收敛。我们还可以看出以下定理:
定理(Policy improvement):如果两个确定性policy \pi,\pi'满足对任意s都有Q _ {\pi}(s,\pi'(s))\geqslant V _ \pi(s),那么\pi'一致地优于\pi,对每一s都有更高的期望return:V _ {\pi'}(s)\geqslant V _ \pi(s)。
Value iteration
在PI中,V和\pi交替更新。而在value iteration (VI)中,这两者是同步的,中间没有显式的policy。
令i=0并初始化V _ 0
V未收敛时执行以下循环:
对每一s:
V _ {k+1}(s)=\max _ a[R(s,a)+\gamma\sum _ {s'}P(s'|s,a)V _ k(s')]循环后计算:\pi(s)=\operatorname{\arg\max} _ a[R(s,a)+\gamma\sum _ {s'}P(s'|s,a)V(s')]
如果引入一个算子B,定义为BV(s)=\max _ a[R(s,a)+\gamma\sum _ {s'}P(s'|s,a)V _ k(s')],那么VI中的迭代也可以看作是V _ {k+1}=BV。事实上这个算子是个压缩映射(\gamma<1),于是根据压缩映射原理,VI也会唯一地收敛——考虑范数\|V-V'\|=\max _ s|V(s)-V(s')|,可以证明\|BV-BV'\|\leqslant\gamma\|V-V'\|。注意到对任两个函数f,g,|\max _ {x} f(x)-\max _ {x}g(x)|\leqslant \max _ x|f(x)-g(x)|(不妨设左边为正,由\max _ x|f(x)-g(x)|+\max _ x|g(x)|\geqslant \max _ x |f(x)|可得)。于是
\begin{aligned}
\|BV-BV'\|&=\max _ s\Big|\max _ a\big[R(s,a)+\gamma\sum _ {s'}P(s'|s,a)V(s')\big]\\&\qquad-\max _ a\big[R(s,a)+\gamma\sum _ {s'}P(s'|s,a)V'(s')\big]\Big|\\
&\leqslant\max _ {s,a}\Big|\gamma\sum _ {s'}P(s'|s,a)(V(s')-V'(s'))\Big|\\
&\leqslant\max _ {s,a}\gamma\sum _ {s'}P(s'|s,a)\|V-V'\|\\&=\gamma\|V-V'\|.
\end{aligned}
Model-free evaluation
本节的model-free evaluation,是指真实MDP未知的情况下对value函数的估计。本节来看V函数。
Monte-Carlo方法
Monte-Carlo方法应用于episode设置下的MDP,即有一个终止state且每一episode必终止。在policy \pi下,V _ {\pi}(s)=E _ {\pi}[G _ t\mid s _ t=s],MC方法的思路即是用经验平均估计期望。
首先是First-visit的MC算法:在每个episode里(均随机生成),如果s第一次出现,进行计数更新和总return更新,N(s)\leftarrow N(s)+1,G(s)\leftarrow G(s)+G _ t,这里return G _ t由r _ t+\gamma r _ {t+1}+\gamma^2r _ {t+2}+\cdots计算,最后以平均进行估计\hat V _ {\pi}(s)=G(s)\mathbin/ N(s)。
Every-visit的MC算法:s的每一次出现,均更新计数和总return,N(s)\leftarrow N(s)+1,G(s)\leftarrow G(s)+G _ t,最后以平均进行估计\hat V _ {\pi}(s)=G(s)\mathbin/ N(s)。
Incremental的MC算法:前面的更新式中,每一次更新如果计算V,那么它由G/N更新到了(G+G _ t)\mathbin/(N+1),或者反过来说由(G-G _ t)\mathbin/(N-1)更新到了G/N,而G/N=\frac1N(G-G _ t+G _ t)=\frac1N[(N-1)V+G _ t]=V+\frac1N(G _ t-V),于是得到incremental的MC算法更新式
V(s)\leftarrow V(s)+\alpha(G _ t-V(s)).如同SGD,\alpha也被叫做学习率。
MC方法的收敛性中,First-visit的收敛比较容易看出,因为各个return都是iid的,由大数定律它们的平均收敛到期望,恰为V函数。另外两个的收敛性不那么显然,可参看其它资料,据称学习率满足经典的\sum _ n\alpha _ n=\infty且\sum _ n\alpha^2 _ n<\infty时算法收敛到真实V函数。
Temporal Difference (TD)
这里只讨论最简单的Temporal difference学习,即TD(0),不讨论更一般的TD(\lambda)。TD可不局限于episode设置下的MDP,在有一组(s,a,r,s')后即可更新:
TD(0)算法:
初始化V(s)\equiv0,然后执行以下循环:
采样(s _ t,a _ t,r _ t,s _ {t+1})
更新V(s _ t)\leftarrow V(s _ t)+\alpha([r _ t+\gamma V(s _ {t+1})]-V(s _ t))
据称:从bias-variance的角度来看,MC高variance零bias,TD低variance些许bias;MC对初始化不敏感,TD更为敏感。
此外,TD利用了Markov结构,因而对数据的利用更有“效率”,而MC可用于非Markov设置下的环境。
Batch MC,TD
本节内容更多讨论可见 Reinforcement Learning An introduction (Second Edition) by Richard S. Sutton and Andrew G. Barto
假设我们有(s _ 1^1,a _ 1^1,r _ 1^1,\dots,s _ {T _ 1}^1),\dots,(s _ 1^K,a _ 1^K,r _ 1^K,\dots,s _ {T _ 1}^K),batch化的算法即是重复采样k\in\{1,\dots,K\},然后对episode k应用MC或TD。
此时batch MC收敛到MSE最小的解,即\sum _ k\sum _ t(G _ t^k-V(s _ t^k))^2最小。而TD(0)收敛到极大似然的解。极大似然是指MDP (\mathcal S,\mathcal A,\hat P,\hat R,\gamma),\hat P(s'|s,a)=\frac1{N(s,a)}\sum _ k \boldsymbol 1(s _ k=s,a _ k=a,s _ {k+1}=s'),\hat r(s,a)=\frac1{N(s,a)}\sum _ k\boldsymbol 1(s _ k=s,a _ k=a)r _ k。这表明如果真实MDP就是(\mathcal S,\mathcal A,\hat P,\hat R,\gamma),那么用TD(0)就跟我们已知该MDP的情况下计算V函数一样。这被称作是certainty-equivalence。
Model-free optimization
本节的model-free optimization,是指真实MDP未知的情况下对value函数的优化。既可以是on-policy的,也可以是off-policy的。前者是指学习和改进的policy是当前正在使用的policy,后者则允许学习过程中使用与当前执行的不同的policy。
如果用V函数来进行policy improvement,那么需要知道MDP的结构:\pi(s)=\operatorname{\arg\max} _ a[R(s,a)+\gamma\sum _ {s'}P(s'|s,a)V(s')]。但用Q函数的话是model-free的:\pi(s)=\operatorname{\arg\max} _ a Q(s,a)。这表明我们可以更多关注Q函数。(尽管如此,对V函数的policy evaluation也是有用的:一方面V函数是单参数,更为简单;还可直接用于比较不同的policy;它让我们对环境和policy的表现都有了更多的理解,是大有裨益的。)
与此同时,因为对环境了解有限,我们要开始面对exploration和exploitation的权衡问题。Exploration是指尝试更多新的action,以发现可能更好的action,这有助于agent更多了解环境,避免局限于当前的已知。Exploitation则是选择已知可以带来高reward的action,有助于稳定地获得reward。最简单的exploration是\epsilon-greedy exploration,是说以\epsilon的概率选择随机action,1-\epsilon的概率根据Q函数选择action。
\pi(a|s)=\begin{cases}\operatorname{\arg\max} _ a Q(s,a),& \text{w.p. }1-\epsilon+\frac{\epsilon}{|\mathcal A|};\\a'\neq\operatorname{\arg\max} _ a Q(s,a),& \text{w.p. }\frac{\epsilon}{|\mathcal A|}.\end{cases}
和前面一样,\epsilon-greedy exploration也是使V函数单调的,这是因为
\begin{aligned}
&Q _ {\pi _ i}(s,\pi _ {i+1}(s))=\sum _ a\pi _ {i+1}(a|s)Q _ {\pi _ i}(s,a)\\
={}&\frac\epsilon{|\mathcal A|}\sum _ a Q _ {\pi _ i}(s,a)+(1-\epsilon)\max _ a Q _ {\pi _ i}(s,a)\\
={}&\frac\epsilon{|\mathcal A|}\sum _ a Q _ {\pi _ i}(s,a)+(1-\epsilon)\frac{1-\epsilon}{1-\epsilon}\max _ a Q _ {\pi _ i}(s,a)\\
\geqslant{}&\frac\epsilon{|\mathcal A|}\sum _ a Q _ {\pi _ i}(s,a)+(1-\epsilon)\sum _ {a\in\mathcal A}\frac{\pi _ i(a|s)-\frac{\epsilon}{|\mathcal A|}}{1-\epsilon}Q _ {\pi _ i}(s,a)\\
={}&\sum _ a\pi _ i(a|s)Q _ {\pi _ i}(s,a)=V _ {\pi _ i}(s),
\end{aligned}由policy improvement定理,\pi _ {i+1}确实优于\pi _ i。
On-policy学习
首先是MC方法。以first-visit的版本为例。
Monte-Carlo Control的算法:
初始化所有Q(s,a),N(s,a),以及\epsilon=1,k=1,执行以下循环:
用policy \pi生成第k个episode (s _ 1,a _ 1,r _ 1,\dots,s _ T,a _ T,r _ T)
如果(s _ t,a _ t)是在该episode首次出现,那么更新:
N(s _ t,a _ t)\leftarrow N(s _ t,a _ t)+1
Q(s _ t,a _ t)\leftarrow Q(s _ t,a _ t)+\frac1{N(s _ t,a _ t)}(G _ t-Q(s _ t,a _ t))
k\leftarrow k+1,\epsilon\leftarrow 1/k用新的Q函数进行policy improvement:
\pi _ k\leftarrow \epsilon\text{-greedy} (Q)
.
这个算法里采用\epsilon-greedy做exploration,使得所有(s,a)都有机会能够出现,与此同时\epsilon不断缩小,使得policy越来越趋近于确定性policy。可以引入一个叫GLIE (Greedy in the Limit of Infinite Exploration)的定义:所有(s,a)无穷多次出现N _ k(s,a)\to\infty,且policy收敛于greedy policy \pi(a|s)\to\operatorname{\arg\max} _ a Q(s,a)。这么看的话GLIE下算法应是收敛到Q^\ast的,但更多细节就不讨论了。
接下来是TD的方法,算法被称作是SARSA算法,因为每次得到一组(s,a,r,s',a')更新一次。
SARSA算法:
初始化……
对每一episode执行以下循环
初始化s _ 1,并根据\pi得到a _ 1,t=1
loop
根据action a _ t行动,得到r _ t,s _ {t+1}
Q(s _ t,a _ t)\leftarrow Q(s _ t,a _ t)+\alpha[r _ t+\gamma Q(s _ {t+1},a _ {t+1})-Q(s _ t,a _ t)]
t\leftarrow t+1,\epsilon\leftarrow 1/t
until s _ t是终止state
.
算法的收敛性不作过多讨论。可参看其它资料:若满足GLIE,且\sum \alpha _ t=\infty,\sum \alpha _ t^2<\infty,那么Q(s,a)\to Q^\ast(s,a),即Q收敛到最优策略的Q函数。
Off-policy学习
现在考虑用不同的behavior policy \mu(a|s)来计算target policy \pi的V _ \pi(s)或Q _ \pi(s,a)。
MC, TD的off-policy学习
off-policy的学习经常需要用到统计学中的重要采样(importance sampling)——要估计\mathbb E _ {\mathrm x\sim p(x)}[f(\mathrm x)],但是要利用更方便的另一个不同的分布q(x),可以重写为:
\mathbb E _ {\mathrm x\sim p(x)}[f(\mathrm x)]=\mathbb E _ {\mathrm x\sim q(x)}\Big[\frac{p(\mathrm x)}{q(\mathrm x)}f(\mathrm x)\Big].
先给出off-policy的Monte-Carlo。在前面,V函数的定义为V _ \pi(s)=E _ \pi[G _ t|s],但现在采用policy \mu的话得到的是E _ \mu[G _ t|s],要利用重要采样,需要计算两个policy的概率商——
\begin{aligned}
\phantom{\implies{}}&\phantom{={}}P _ \pi(a _ t,s _ {t+1},a _ {t+1},\dots,s _ T\mid s _ t)=\\
\phantom{\implies{}}&{={}}P _ \pi(a _ t|s _ t)P _ \pi(s _ {t+1}|s _ t,a _ t)P _ \pi(a _ {t+1}|s _ {t+1})\cdots P _ \pi(s _ T|s _ {T-1},a _ {T-1})\\
\phantom{\implies{}}&{={}}\prod _ {k=t}^{T-1}\pi(a _ k|s _ k)P(s _ {k+1}|s _ k,a _ k).\\
\implies{}&\frac{P _ \pi}{P _ \mu}=\prod _ {k=t}^{T-1}\frac{\pi(a _ k|s _ k)}{\mu(a _ k|s _ k)}.
\end{aligned}我们需要限制\pi(a|s)>0时\mu(a|s)>0,这表明\mu\neq\pi时\mu必然不是确定性的policy(而target policy一般设置为确定性的)。
用重要采样估计V函数的off-policy的Monte-Carlo的算法:
更新式变更为
V(s _ t)\leftarrow V(s _ t)+\alpha(\frac{P _ \pi}{P _ \mu}G _ t-V(s _ t))
.
而off-policy的Temporal difference则完全类似。
用重要采样估计V函数的off-policy的Temporal difference的算法:
更新式变更为
V(s _ t)\leftarrow V(s _ t)+\alpha[\frac{P _ \pi}{P _ \mu}(r _ {t+1}+\gamma V(s _ {t+1}))-V(s _ t)]
Q-learning
对于Q函数的off-policy学习,一般称作是Q-learning。此时不再需要重要采样。
我们将target policy \pi设置为greedy policy:\pi(s _ {t})=\operatorname{\arg\max} _ a Q(s _ t,a)=\tilde a,而behavior policy设置为\epsilon-greedy policy:\mu(s _ t)=\epsilon-greedy (Q),这样
\begin{aligned}
r _ {t+1}+\gamma Q(s _ {t+1},\tilde a)&=r _ {t+1}+\gamma Q(s _ {t+1},\operatorname*{\arg\max} _ {a'}Q(s _ {t+1},a'))\\
&=r _ {t+1}+\max _ {a'}\gamma Q(s _ {t+1},a').
\end{aligned}于是得到以下算法。
Q-learning算法:
SARSA中的loop改为
根据action a _ t行动,得到r _ t,s _ {t+1}
Q(s _ t,a _ t)\leftarrow Q(s _ t,a _ t)+\alpha[r _ t+\gamma\max _ a Q(s _ {t+1},a)-Q(s _ t,a _ t)]
t\leftarrow t+1,\epsilon\leftarrow 1/t
.
算法的收敛性不作过多讨论。可参看其它资料:若能使所有(s,a)无穷多次出现,且\sum \alpha _ t=\infty,\sum \alpha _ t^2<\infty时,Q(s,a)\to Q^\ast(s,a);如果额外令\epsilon _ t使得GLIE成立,那么policy收敛到\pi^\ast。
近似V函数或Q函数
利用 deep reinforcement learning
从这里开始,我们会关注能用于解决规模比较大的问题的方法。当|\mathcal S|巨大的时候,对所有V(s),Q(s,a)的储存和计算都十分困难。而这种情况在实际中是比比皆是,因而我们需要退而求其次。在计算条件有限的情况下我们可以尽量找近似解,例如近似V函数或Q函数,下面以Q函数为例。如果Q(s,a)是已知的,那么这就化归到了一个回归问题,数据为\{((s _ i,a _ i),Q(s _ i,a _ i))\}。使用神经网络是一种可行的选择,这样我们不需要关于环境的先验知识来设计特征。用\hat Q(s,a;\boldsymbol \theta)来近似Q函数,用SGD等优化算法,最小化(经验)均方损失\frac1{2n}\sum[Q(s _ i,a _ i)-\hat Q(s _ i,a _ i;\boldsymbol \theta)]^2即可。
当然我们需要考虑真实Q(s,a)并非已知的情况。和前面类似,将其适当替代即可:
- MC方法中,以return G _ t代替Q(s,a);
- 在SARSA中,以r+\gamma\hat Q(s',a';\boldsymbol \theta)代替Q(s,a);
- 在Q-learning中,以r+\gamma\max _ {a'}\hat Q(s',a';\boldsymbol\theta)代替Q(s,a)。
Deep Q-Networks (DQN)
深度强化学习在Atari上的成功使其吸引了大量注意,可见:
MNIH, Volodymyr, et al. Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602, 2013.
可称作是深度Q学习,其中的网络则是Deep Q-Networks (DQN)。其中的算法有两个做法十分重要:experience replay以及fixed Q-targets。Experience replay的做法是采用一个储存了最近N个(s _ t,a _ t,r _ t,s _ {t+1})的buffer,然后神经网络的每次迭代是从这个buffer里面随机采样一个minibatch,来进行梯度更新。这种做法减小了相邻样本间的correlation,于是提升了稳定性。Fixed Q-targets则是提升稳定性的另一种措施:一种不稳定性是由label依赖于网络参数导致,每次迭代后label都会发生变化,而对均方损失求导时我们一般是将label视为与网络参数独立的常量的。在DQN里,优化\hat Q(s,a;\boldsymbol\theta _ k)时,每个minibatch里的label是暂时“固定”为r+\gamma\max _ {a'}\hat Q(s',a';\boldsymbol\theta _ {k-1})的。这样就是最小化\frac1{2n}\sum[r _ i+\gamma\max _ {a}\hat Q(s _ i,a;\boldsymbol\theta _ {k-1})-\hat Q(s _ i,a _ i;\boldsymbol\theta _ k)]^2。
DQN的一种简单变体则是Double DQN。在Q-learning里,前面我们已经知道label可写成r _ {t+1}+\gamma Q(s _ {t+1},\operatorname*{\arg\max} _ {a'}Q(s _ {t+1},a'))的形式,里层的Q函数用于确定policy,外层的Q则用于确定V;在Double DQN里,这两个Q被解耦,label变为了
r _ t+\gamma \hat Q(s _ t,\operatorname*{\arg\max} _ a\hat Q(s _ {t+1},a;\boldsymbol \theta _ {k});\boldsymbol \theta _ {k-1}).可见:
Van Hasselt, Hado, Arthur Guez, and David Silver. "Deep reinforcement learning with double q-learning." Proceedings of the AAAI conference on artificial intelligence. Vol. 30. No. 1. 2016.
Policy gradient Ⅰ
本节我们关注直接对policy建模然后从中选择的方法。很多时候直接考虑policy比考虑V函数或Q函数都要简单,而且V函数不直接包含action的信息,从中得到最优policy还需要额外的一轮计算,从Q函数中得到最优policy也需要解\operatorname{\arg\max} _ a Q(s,a)。此外,我们还可以在建模policy的过程中直接加入关于期待policy的先验知识。因此,直接建模policy然后从中找出最优者,是自然的想法。
为了对policy进行比较、排序,我们需要确定policy的评估准则 衡量标准。在RL里的两种问题设置下,或有些许区分。
Episodic任务和continuing任务
在Episodic设置下,有一个终止state,数据被自然分为一个个episode,且新的episode与旧的独立;另一种情况,无法分为episodes,agent一直持续地与环境互动,这种设置称为continuing设置。
先考虑在continuing设置下,对评估准则的确定。固定一个policy \pi,我们得到一个Markov链。我们假设这个Markov链(无论固定何种policy)总是irreducible、positive recurrent、aperiodic的,这样根据前文回顾的收敛定理,无论初始state如何,最终都会收敛到平稳分布\mu _ \pi,按照定义它满足
\sum _ s \mu _ \pi(s)\sum _ a \pi(a|s)P(s'|s,a)=\mu _ \pi(s').这样初始state的选择、早期agent的表现就不那么重要了。长期地看,我们更应关注每个时间步的平均reward,用字母\bar r(\pi)表示:
\begin{aligned}
J _ 1(\pi)=\bar r(\pi)&=\lim _ {T\to\infty}\frac1T\sum _ {t=1}^T E _ {\pi}[r _ t|s _ 0]=\lim _ {t\to\infty}E _ \pi[r _ t|s _ 0]\\
&=\lim _ {t\to\infty}E _ {\pi}[r(s,a)|s _ 0]\\
&=\sum _ s\mu _ \pi(s)\sum _ a \pi(a|s) R(s,a).
\end{aligned}也可以关注平稳后每个state的V函数值的平均,仍用J表示:
J _ 2(\pi)=\sum _ s\mu _ \pi(s)V _ \pi(s).
这两种J本质上都是一样的,这是因为
\begin{aligned}
J _ 2(\pi)&=\sum _ s\mu _ \pi(s)\sum _ a\pi(a|s)\Big(R(s,a)+\gamma\sum _ {s'}P(s'|s,a)V _ \pi(s')\Big)\\
&=J _ 1(\pi)+\gamma\sum _ s\mu _ \pi(s)\sum _ a\pi(a|s)\sum _ {s'} P(s'|s,a)V _ \pi(s')\\
&\stackrel{(\ast)}=J _ 1(\pi)+\gamma \sum _ {s'}V _ \pi(s')\mu _ \pi(s')=J _ 1(\pi)+\gamma J _ 2(\pi)\phantom{\sum _ s}\\
(1-\gamma)J _ 2(\pi)&=J _ 1(\pi)\phantom{\sum}\\
J _ 2(\pi)&=\frac1{1-\gamma}J _ 1(\pi).
\end{aligned}其中(*)利用了前面的平稳分布性质。由于二者只相差一个常数因子,因此(无论\gamma取何值)对policy的比较、排序都是一致的。
在continuing设置下,经常会考虑另一种value函数,它们定义为
\begin{aligned}V _ \pi^\delta(s)&=E _ \pi[(r _ t-\bar r(\pi))+(r _ {t+1}-\bar r(\pi))+\cdots\mid s _ t=s] \\Q _ \pi^\delta(s)&=E _ {\pi}[(r _ t-\bar r(\pi))+(r _ {t+1}-\bar r(\pi))+\cdots\mid s _ t=s, a _ t=a],\end{aligned}其中\bar r(\pi)表示前面定义的policy \pi之下平均每个时间步的平均reward。可以看到除了将reward r _ t换为了r _ t-\bar r(\pi),还去掉了用于discount的\gamma。这种定义不改变value函数间的相对值:
V _ \pi^\delta(s _ 1)-V _ \pi^\delta(s _ 2)=V _ \pi(s _ 1)-V _ \pi(s _ 2). V函数和Q函数间的关系利用条件期望的性质,可发现仍有
V _ \pi^\delta(s)=\sum _ a\pi(a|s)Q^\delta _ \pi(s,a).也不难推出和原来类似的递推关系(R变为了R-\bar r):
\begin{aligned}
V _ \pi^\delta(s)&=\sum _ a \pi(a|s)\Big(R(s,a)-\bar r(\pi)+\sum _ {s'}P(s'|s,a)V _ \pi^\delta(s')\Big)\\
Q _ \pi^\delta(s,a)&=R(s,a)-\bar r(\pi)+\sum _ {s'}P(s'|s,a)V _ \pi^\delta(s')\\
&=R(s,a)-\bar r(\pi)+\sum _ {s'}P(s'|s,a)\sum _ {a'}\pi(a'|s')Q _ \pi^\delta(s',a').
\end{aligned}这种定义对后面的policy gradient定理大有裨益。
对于episode设置,如果有一个明确的“开始”state s _ 0,我们总可以将它作为episode的初始,因此只需要考虑V _ \pi(s _ 0)就可以了,这种情况下我们令J(\pi)=V _ \pi(s _ 0)。在没有这样的state的情况下,也可以像前面一样,采用和continuing设置一样的J(\pi)。
Policy gradient 方法
总体思路
如前文所说,我们要直接建模policy,考虑建模为以\boldsymbol \theta为参数的模型\pi(a|s,\boldsymbol\theta),然后为了符号的简洁我们把J(\pi)改记为\boldsymbol\theta 的函数J(\boldsymbol\theta)。一旦建模好了,就来到了一个优化问题
\operatorname*{\arg\max} _ {\boldsymbol\theta} J(\boldsymbol\theta).诸多优化算法可以选择,但如果能求梯度,用基于梯度的方法比不需梯度的方法理应是更有效率的。这些方法一般称作是policy gradient方法。这里考虑如下思路:
\boldsymbol\theta\leftarrow\boldsymbol\theta+\alpha\nabla J(\boldsymbol\theta).有些方法除了学习policy还会学习value函数,一般称为是actor-critic方法——actor对应学习的policy,critic对应学习的value函数。
Policy的建模
假设我们现在能够计算梯度,那么只剩下如何对policy的(可微)建模的问题。对于离散的action \mathcal A,可以采用softmax policy,简单的做法是
\pi(a|s;\boldsymbol \theta)=\mathsf{softmax}(\boldsymbol \phi(s,a)^\mathsf T\boldsymbol \theta)=\frac{\exp(\boldsymbol \phi(s,a)^\mathsf T\boldsymbol \theta)}{\sum _ {a'}\exp(\boldsymbol \phi(s,a')^\mathsf T\boldsymbol \theta)}.考虑神经网络也是可行的:
\pi(a|s;\boldsymbol \theta)=\mathsf {softmax}(\phi _ {\mathrm{NN}}(s,a,\boldsymbol \theta)).
而对于连续的action,可以用正态分布建模:
\begin{aligned}\pi(a|s;\boldsymbol \theta)&=\mathcal N(a;\mu(s,\boldsymbol \theta),\sigma^2(s,\boldsymbol \theta))\\
&=\frac1{\sqrt{2\pi\sigma^2(s,\boldsymbol \theta)}}\exp\Big(-\frac1{2\sigma^2(s,\boldsymbol \theta)}[a-\mu(s,\boldsymbol \theta)]^2\Big).
\end{aligned}
这些建模的policy都可以显式地求导\nabla\pi(a|s,\boldsymbol\theta)。而且,由于所有action都有正概率,我们兼顾了policy的exploration。
Policy gradient 定理
现在需要回到policy gradient的计算问题。对\nabla J(\boldsymbol \theta)的计算需要知道充分的环境的知识,很多时候是做不到的。而下面的policy gradient定理表明我们有一个行之有效的方法计算梯度。
定理(Policy gradient, episodic):令J(\pi)=V _ \pi(s _ 0),则J(\pi)对\boldsymbol \theta的梯度在适当条件下满足
\begin{aligned}
\nabla J(\boldsymbol \theta)&\propto \sum _ s\rho _ \pi(s)\sum _ aQ _ \pi(s,a)\nabla \pi(a|s;\boldsymbol \theta)\\
&=E _ {s\sim\rho}E _ {a\sim\pi(a|s)}[Q _ \pi(s,a)\nabla\ln\pi(a|s;\boldsymbol \theta)].
\end{aligned}
这里的分布\rho _ \pi(s)在下面定义。无论是softmax policy还是正态policy,\pi(a|s;\boldsymbol\theta)都是严格正的数,因而取对数是没有问题的。
定理中的等式用到了
\sum _ a\nabla\pi(a|s)=\sum _ a\pi(a|s)\frac{\nabla\pi(a|s)}{\pi(a|s)}=\sum _ a\pi(a|s)\nabla\ln\pi(a|s).
下面给出这个定理的证明。(可选择跳过阅读此部分)
在此之前,我们需要一个记号简化书写。用P(s _ 0\stackrel{t=k}\to s')表示从s _ 0出发,在policy \pi下经过k步后到达的state是s'的概率,这样在k充分大之后一般会接近于平稳分布的值\mu _ \pi(s')。然后记\phi(s)=\sum _ a\nabla\pi(a|s)Q _ \pi(s,a)。
先考虑J(\pi)=V _ \pi(s _ 0)的情况。首先将V函数用Q函数表示,然后用乘法的求导法则,再用V函数表示Q函数,这样就得到了一个递推式,然后就可以利用这个递推式无限展开:
\begin{aligned}
&\nabla J(\boldsymbol\theta)=\nabla V _ \pi(s _ 0)=\nabla\Big(\sum _ a\pi(a|s _ 0)Q _ \pi(s _ 0,a)\Big)\\
={}&\sum _ a\Big(\nabla\pi(a|s _ 0)Q _ \pi(s _ 0,a)+\pi(a|s _ 0)\nabla Q _ \pi(s _ 0,a)\Big)\\
={}&\phi(s _ 0)+\sum _ a\Big[\pi(a|s _ 0)\nabla \Big(R(s _ 0,a)+\gamma\sum _ {s _ 1}P(s _ 1|s _ 0,a)V _ \pi(s _ 1)\Big)\Big]\\
={}&\phi(s _ 0)+\sum _ a\pi(a|s _ 0)\sum _ {s _ 1}\gamma P(s _ 1|s _ 0,a)\nabla V _ \pi(s _ 1)\\
={}&\phi(s _ 0)+\sum _ {s _ 1}\gamma P(s _ 0\stackrel{t=1}\to s _ 1)\nabla V _ \pi(s _ 1)\\
={}&\phi(s _ 0)+\sum _ {s _ 1}\gamma P(s _ 0\stackrel{t=1}\to s _ 1)\phi(s _ 1)+\sum _ {s _ 2}\gamma^2 P(s _ 0\stackrel{t=2}\to s _ 2)\nabla V _ \pi(s _ 2)\\
={}&\cdots=\sum _ {k=0}^\infty\sum _ {s\in\mathcal S}\gamma^k P(s _ 0\stackrel{t=k}\to s)\phi(s).
\end{aligned}现在我们需要一个额外的条件:上面最后的表达式两个求和号可以互换(不难成立)。这样
\begin{aligned}
\nabla J(\boldsymbol\theta)&=\sum _ {s\in\mathcal S}\phi(s)\sum _ {k=0}^\infty\gamma^kP(s _ 0\stackrel{t=k}\to s)\\
&:=\sum _ {s\in\mathcal S}\frac1{1-\gamma}\rho _ \pi(s)\phi(s)\\
&=\sum _ {s}\frac1{1-\gamma}\rho _ \pi(s)\sum _ aQ _ \pi(s,a)\nabla \pi(a|s)\\
&\propto\sum _ s\rho _ \pi(s)\sum _ aQ _ \pi(s,a)\nabla\pi(a|s).
\end{aligned}其中定义了\rho _ \pi(s)=(1-\gamma)\sum _ {k=0}^\infty\gamma^kP(s _ 0\stackrel{t=k}\to s)。可以证明\rho _ \pi确实是\mathcal S上的分布:对任意的s,级数项都是非负的,因此\sum _ s\rho _ \pi(s)=(1-\gamma)\sum _ {k=0}^\infty\gamma^k=1。于是我们证明了J=V _ \pi(s _ 0)情况下的定理。
证明中可以看到,分布\rho为
\rho _ \pi(s)=(1-\gamma)\sum _ {k=0}^\infty\gamma^k P(s _ 0\stackrel{t=k}\to s).一般称作discounted state distribution。在实际应用中,却并不容易直接对s从这个分布采样,因而实现上会略有不同。可见下面推导的REINFORCE算法。
在continuing设置下,通过利用另一种定义的value函数,我们可以不再理会\gamma的作用,s的分布也变为了平稳分布。
定理(Policy gradient, continuing):令J(\pi)=\bar r(\pi)=\sum _ s\mu _ \pi(s)\sum _ a \pi(a|s) R(s,a),则J(\pi)对\boldsymbol \theta的梯度满足
\begin{aligned}\nabla J(\boldsymbol \theta)&=\sum _ s\mu _ \pi(s)\sum _ aQ^\delta _ \pi(s,a)\nabla \pi(a|s;\boldsymbol \theta)\\&=E _ {s\sim\mu,a\sim\pi}[Q^\delta _ \pi(s,a)\nabla\ln\pi(a|s;\boldsymbol \theta)].\end{aligned}这里的分布\mu _ \pi(s)是平稳分布。
下面证明J(\pi)=\sum _ s\mu _ \pi(s)\sum _ a \pi(a|s) R(s,a)的情况。(可选择跳过阅读此部分)
注意到平稳分布\mu _ \pi满足\sum _ s \mu _ \pi(s)\sum _ a \pi(a|s)P(s'|s,a)=\mu _ \pi(s'),我们有
\begin{aligned}
&Q _ \pi^\delta(s,a)=R(s,a)-\bar r(\pi)+\sum _ {s'}P(s'|s,a)V _ \pi^\delta(s')\\
\implies{}&\nabla Q _ \pi^\delta(s,a)=-\nabla\bar r(\pi)+\sum _ {s'}P(s'|s,a)\nabla V _ \pi^\delta(s')\\
&V _ \pi^\delta(s)=\sum _ a\pi(a|s)Q _ \pi^\delta(s,a)\\
\implies{}&\nabla V _ \pi^\delta(s)=\sum _ a\nabla\pi(a|s)Q _ \pi^\delta(s,a)+\sum _ a\pi(a|s)\nabla Q _ \pi^\delta(s,a)\\
\implies{}&\nabla V _ \pi^\delta(s)=\sum _ a\nabla\pi(a|s)Q _ \pi^\delta(s,a)\\
&\qquad+\sum _ a\pi(a|s)[-\nabla\bar r(\pi)+\sum _ {s'}P(s'|s,a)\nabla V _ \pi^\delta(s')]\\
\implies{}&\sum _ s\mu _ \pi(s)\nabla V _ \pi^\delta(s)=\sum _ s\mu _ \pi(s)\sum _ a\nabla\pi(a|s)Q _ \pi^\delta(s,a)\\
&\qquad+\sum _ s\mu _ \pi(s)\sum _ a\pi(a|s)[-\nabla\bar r(\pi)+\sum _ {s'}P(s'|s,a)\nabla V _ \pi^\delta(s')]\\
\implies{}&\sum _ s\mu _ \pi(s)\nabla V _ \pi^\delta(s)=\sum _ s\mu _ \pi(s)\sum _ a\nabla\pi(a|s)Q _ \pi^\delta(s,a)\\
&\qquad-\nabla\bar r(\pi)+\sum _ {s'}\mu _ \pi(s')\nabla V _ \pi^\delta(s')\\
\implies{}&\nabla\bar r(\pi)=\sum _ s\mu _ \pi(s)\sum _ a\nabla\pi(a|s)Q _ \pi^\delta(s,a).
\end{aligned}这就证明了定理。
REINFORCE算法
REINFORCE算法即Monte Carlo policy gradient算法。
一般推导
在episode设置下,由E _ \pi[G _ t|s _ t,a _ t]=Q _ \pi(s _ t,a _ t),我们将\nabla J(\boldsymbol\theta)写成
\begin{aligned}
&\sum _ {k=0}^\infty \Big[\sum _ {s\in\mathcal S}P(s _ 0\stackrel{t=k}\to s)\sum _ a\gamma^k Q _ \pi(s,a)\nabla \pi(a|s)\Big]\\
={}&\sum _ {k=0}^\infty E _ {\pi}\Big[\sum _ a\gamma^kQ _ \pi(s _ k,a)\nabla\pi(a|s _ k)\Big]\\
={}&\sum _ {k=0}^\infty E _ \pi[\gamma^k G _ k\nabla\ln\pi(a|s _ k)].
\end{aligned}参数更新时可以把这些k的项拆开,逐项更新。于是,我们可以考虑如下的参数更新:
\boldsymbol\theta\leftarrow\boldsymbol\theta+\alpha\cdot \gamma^t G _ t\nabla \ln\pi(a _ t|s _ t;\boldsymbol\theta).
REINFORCE算法:
适当初始化,然后执行以下循环
按\pi(a|s,\boldsymbol\theta)生成episode s _ 0,a _ 0,r _ 0,\dots,s _ {T},a _ T,r _ T,s _ {T+1}
for t=0 to T do
\boldsymbol\theta\leftarrow\boldsymbol\theta+\alpha\cdot \gamma^tG _ t\nabla\ln\pi(a _ t|s _ t;\boldsymbol\theta)
end for
Continuing设置下则完全类似,不多叙述了。可以用经验平均进行估计,例如\frac1T\sum _ {i=0}^T r _ i\approx\bar r(\pi),进而得到Q _ \pi^\delta(s,a)的近似。
有限horizon
如果只考虑有限horizon的return E _ {\pi}[\sum _ {t=0}^H \gamma^t r(s _ t,a _ t)],推导更清晰明了。我们令\boldsymbol\tau=(s _ 0,a _ 0,r _ 0,\dots,a _ {H},r _ H,s _ {H+1}),return写成E _ \pi[R(\boldsymbol\tau)]=\sum _ {\boldsymbol\tau} P(\boldsymbol\tau;\boldsymbol\theta)R(\boldsymbol\tau)。这样求梯度就是
\begin{aligned}
\nabla E _ \pi[R(\boldsymbol\tau)]=\sum _ {\boldsymbol\tau}\nabla P(\boldsymbol\tau;\boldsymbol\theta)R(\boldsymbol\tau)&=\sum _ {\boldsymbol\tau} P(\boldsymbol\tau;\boldsymbol\theta)R(\boldsymbol\tau)\nabla\ln P(\boldsymbol\tau;\boldsymbol\theta)\\
&=E _ \pi[R(\boldsymbol\tau)\nabla\ln P(\boldsymbol\tau;\boldsymbol\theta)].
\end{aligned}对于\ln P(\boldsymbol\tau;\boldsymbol\theta)的梯度,有
\nabla \ln P(\boldsymbol\tau;\boldsymbol\theta)=\nabla\ln\Big[P(s _ 0)\prod _ {t=0}^H\pi(a _ t|s _ t)P(s _ {t+1}|s _ t,a _ t)\Big]=\sum _ {t=0}^H \nabla\ln\pi(a _ t|s _ t).因此,
\nabla E _ \pi[R(\boldsymbol\tau)]=E _ \pi\Big[R(\boldsymbol\tau)\sum _ {t=0}^H\nabla\ln\pi(a _ t|s _ t)\Big]=E _ \pi\Big[\sum _ {t'=0}^H\gamma^{t'} r(s _ {t'},a _ {t'})\sum _ {t=0}^H\nabla\ln\pi(a _ t|s _ t)\Big].按这种思路,我们可以先把R(\boldsymbol\tau)=\sum _ {t=0}^H \gamma^t r(s _ t,a _ t)的项拆开:
\begin{aligned}
&\nabla E _ \pi[\gamma^{t'} r(s _ {t'},a _ {t'})]=E _ \pi\Big[\gamma^{t'}r(s _ {t'},a _ {t'})\sum _ {t=0}^{t'}\nabla\ln\pi(a _ t|s _ t)\Big]\\
\implies{}&\phantom{={}}\nabla E _ \pi[R(\boldsymbol\tau)]=E _ \pi\Big[\sum _ {t'=0}^H\gamma^{t'} r(s _ {t'},a _ {t'})\sum _ {t=0}^{t'}\nabla\ln\pi(a _ t|s _ t)\Big]\\
&{={}}E _ \pi\Big[\sum _ {t=0}^{H}\sum _ {t'=t}^H\gamma^{t'} r(s _ {t'},a _ {t'})\nabla\ln\pi(a _ t|s _ t)\Big]\\
&{={}}\sum _ {t=0}^HE _ \pi[\gamma^{t}G _ t\nabla\ln\pi(a _ t|s _ t)].
\end{aligned}我们再一次得到了REINFORCE的参数更新
\boldsymbol\theta\leftarrow\boldsymbol\theta+\alpha\cdot \gamma^t G _ t\nabla \ln\pi(a _ t|s _ t;\boldsymbol\theta).
Baseline
虽然前面采用的参数更新是无偏的,但方差可能比较大,通常会考虑引入baseline降低。前面已经推出\nabla J(\boldsymbol\theta)=\sum _ {k=0}^\infty E _ \pi[\gamma^k Q _ \pi(s _ k,a _ k)\nabla\ln\pi(a _ k|s _ k)],注意到E _ a[b\cdot\nabla\ln\pi(a|s)]=\sum _ ab\cdot\nabla\pi(a|s)=b\cdot\nabla\sum _ a\pi(a|s)=0,因此梯度可改写为
\nabla J(\boldsymbol\theta)=\sum _ {k=0}^\infty E _ \pi[\gamma^t(Q _ \pi(s _ t,a _ t)-b(\boldsymbol s))\nabla\ln\pi(a _ t|s _ t))].因而一个比较好的选择应是b=E _ a[Q _ \pi(s _ t,a)]=V _ \pi(s _ t)(概率统计中,熟知\mathbb E(\mathrm x)使得\mathbb E _ {\mathrm x}[(\mathrm x-\cdot)^2]最小),我们得到一个被称作是advantage函数的函数:
A _ \pi(s,a)=Q _ \pi(s,a)-V _ \pi(s).
一种算法如下。
带baseline的policy gradient算法:
适当初始化后,执行以下循环
按\pi(a|s,\boldsymbol\theta)生成第i个episode s _ 0,a _ 0,r _ 0,\dots,s _ {T},a _ T,r _ T,s _ {T+1}
for t=0 to T do
计算advantage的估计\hat A _ t=G _ t-b(s _ t)
更新baseline b(s _ t)=\operatorname{\arg\min} _ b\sum _ i\sum _ t|b(s^{(i)} _ t)-G _ t^{(i)}|^2
更新参数\boldsymbol\theta\leftarrow\boldsymbol\theta+\alpha\cdot \gamma^t\hat A _ t\nabla\ln\pi(a _ t|s _ t;\boldsymbol\theta)
end for
Actor-critic方法:A3C
除了baseline,我们还可以引入critic学习value函数。仿照TD(0),advantage函数的估计是r _ t+\gamma\hat V(s _ {t+1})-\hat V(s _ t),而前面的MC式估计则是r _ t+\gamma r _ {t+1}+\gamma^2t _ {t+2}+\dots-\hat V(s _ t)。前面已提及TD(0)低variance高bias,MC高variance低bias,因此可以选择一个中间的平衡点,以达成bias-variance tradeoff。可以参考下面A3C(Asynchronous Advantage Actor-Critic)的算法。
A3C是2016年提出的流行actor-critic算法:
MNIH, Volodymyr, et al. Asynchronous methods for deep reinforcement learning. In: International conference on machine learning. PMLR, 2016. p. 1928-1937.
A3C算法思路:
Critic将学习一个V函数\hat V(s;\boldsymbol\theta _ v)
循环以下步骤
Agent行动T步(例如,T=20)
for t=0 to T
\hat Q _ t=r _ t+\gamma r _ {t+1}+\dots+\gamma^{T-1-t}r _ {T-1}+\gamma^{T-t}\hat V(s _ {t+1})
\hat A _ t=\hat Q _ t-\hat V(s _ t)
更新参数
\boldsymbol\theta\leftarrow\boldsymbol\theta+\alpha _ 1\sum _ {t=0}^{T}\gamma^t\hat A _ t\nabla _ {\boldsymbol\theta}\ln\pi(a _ t|s _ t;\boldsymbol\theta)
\boldsymbol\theta _ c\leftarrow\boldsymbol\theta _ c-\alpha _ 2\sum _ {t=0}^{T}\nabla _ {\boldsymbol\theta _ c}[\hat A _ t-\hat V(s _ t;\boldsymbol\theta _ c)]^2
Policy gradient Ⅱ
这一节我们主要关注PPO算法(Proximal Policy Optimization)。
Proximal Policy Optimization (PPO) 是一种较为现代的方法,在训练ChatGPT的过程中就有所应用,当下十分流行。下面对其背后的一些可能的启发性想法大致叙述。由于技术细节较多,可仅观其大略。内容主要来自 Lecture on advanced policy gradient methods (PPO/TRPO)
一些推导过程改编自如下论文:
ACHIAM, Joshua, et al. Constrained policy optimization. In: International conference on machine learning. PMLR, 2017.
KL散度与policy optimization
一般来说,Policy gradient的问题在于我们每次更新是在参数上的更新,然后再作用到policy上。因而更新步长直接影响更新好坏,而且policy的参数化方式也会有所影响。例如用sigmoid函数做决策,参数为0时\sigma(0)=0.5,为2时\sigma(2)\approx0.88,为4时\sigma(4)\approx0.98——参数空间上变化和policy空间上的甚至可以很不同。而下面的分析是从直接的policy优化出发的,以规避参数化带来的影响。
下面仍考虑episode设置。
Policy Performance Bounds
引理(Relative policy performance identity):对任意两个policy \pi,\pi'有
J(\pi')-J(\pi)=E _ {\pi'}\Big[\sum _ {t=0}^\infty\gamma^t A _ \pi(s _ t,a _ t)\Big].
我们从右边推到左边。右边为E _ {\pi'}[\sum _ t \gamma^t(R(s _ t,a _ t)+\gamma V _ \pi(s _ {t+1})-V _ \pi(s _ t))],而第一项E _ {\pi'}[\sum _ {t}\gamma^t R(s _ t,a _ t)]=J(\pi'),第二项为E _ {\pi'}[\sum _ t\gamma^{t+1} V _ \pi(s _ {t+1})]=E _ {\pi'}[\sum _ {t=1}^\infty\gamma^{t} V _ \pi(s _ {t})],恰好跟第三项几乎都抵消,只剩下-E _ {\pi'}[V _ \pi(s _ 0)]=-J(\pi),这就证明了引理。
假设现在我们有policy \pi,要找新的policy \pi',只需要对J(\pi')-J(\pi)作优化,即\operatorname{\arg\max} _ {\pi'}(J(\pi')-J(\pi))。再从这个引理,我们需要policy \pi'使得\sum _ t\gamma^t A _ \pi(s _ t,a _ t)的期望最大。
利用前面policy gradient定理里定义的discounted state distribution,即\rho _ \pi(s)=(1-\gamma)\sum _ {k=0}^\infty\gamma^k P(s _ 0\stackrel{t=k}\to s),我们把右边进一步改写。将E _ {\pi'}[\sum _ t\gamma^t A _ \pi(s _ t,a _ t)]写成\sum _ {k=0}^\infty\sum _ {s}P(s _ 0\stackrel{t=k}\to s)\sum _ {a}\pi'(a|s)\gamma^k A _ \pi(s,a),交换求和号的顺序,就是\frac1{1-\gamma}E _ {s\sim\rho _ {\pi'},a\sim\pi'}[A _ \pi(s,a)],利用重要采样的方法(见前文),现在变成
J(\pi')-J(\pi)=\frac1{1-\gamma}E _ {s\sim\rho _ {\pi'},a\sim\pi}\Big[\frac{\pi'(a|s)}{\pi(a|s)}A _ \pi(s,a)\Big].期望是对s\sim\rho _ {\pi'}求的,而我们希望对\rho _ {\pi}求期望,这样数据可以只从\pi产生。
我们可以对“直接用\rho _ {\pi}而非\rho _ {\pi'}来近似”所造成的误差进行估计。首先来估计\rho _ {\pi'}-\rho _ \pi,下面的引理表明,可以用KL散度D _ {\mathrm{KL}}(\pi'\|\pi)来bound住\sum _ s|\rho _ {\pi'}(s)-\rho _ \pi(s)|。
引理:
\|\rho _ {\pi'}-\rho _ \pi\| _ 1\leqslant E _ {s\sim\rho _ \pi}\sqrt{2D _ {\mathrm {KL}}(\pi\|\pi')(s)}.
现在给出这个引理的证明。可选择跳过阅读此部分。
设p(s)是\mathcal S上的任意一个分布(或者只要求是\mathcal S上的一个函数),算子\mathcal P:p\mapsto\mathcal Pp表示初始state分布为p时经过policy \pi的一次行动后的分布,写出来就是\mathcal Pp(s')=\sum _ {s}P(s'|s)p(s)。类似地,算子\mathcal Q:p\mapsto\mathcal Qp利用discounted state distribution定义:\mathcal Qp(s')=\sum _ s p(s)\sum _ k(1-\gamma)\gamma^k P(s\stackrel{t=k}\to s')。
考察\mathcal{PQ}p,按定义\mathcal{PQ}p(\cdot)=\sum _ {s'} P(\cdot|s')\sum _ s p(s)\sum _ k(1-\gamma)\gamma^kP(s\stackrel{t=k}\to s'),注意到\sum _ {s'} P(\cdot|s')P(s\stackrel{t=k}\to s')=P(s\stackrel{t=k+1}\longrightarrow \cdot),有\gamma\mathcal{PQ}p(\cdot)=\sum _ s p(s)\sum _ k(1-\gamma)\gamma^{k+1}P(s\stackrel{t=k+1}\to \cdot),和\mathcal Qp(\cdot)相比,后者多了一项\sum _ sp(s)(1-\gamma) P(s\stackrel{t=0}\to\cdot)=(1-\gamma)p(\cdot),这表明(\mathcal Q-\gamma\mathcal {PQ})p=(1-\gamma)p。同样的计算可以得知(\mathcal{Q}-\gamma\mathcal{QP})p=(1-\gamma )p。
对policy \pi',我们定义类似的\mathcal P',\mathcal Q'(这里用符号(\prime)表示对\pi的定义应用到\pi',同理P'(\tilde s|s):=P(\tilde s|s;\pi'),依此类推)。那么(1-\gamma)(\mathcal Q'-\mathcal Q)=\mathcal Q'(\mathcal Q-\gamma\mathcal{PQ})-(\mathcal Q'-\gamma\mathcal{Q}'\mathcal{P}')\mathcal Q=\gamma\mathcal Q'(\mathcal P-\mathcal P')\mathcal Q,这个等式连接了\mathcal Q'-\mathcal Q和\mathcal P-\mathcal P'。由于在episode设置下我们总是取s _ 0作为初始state,因此可以考虑在前面的p取为s _ 0上的Dirac delta函数:p=\delta _ {s _ 0},这样\rho _ \pi(s)=\mathcal Qp(s),估计\rho _ {\pi'}-\rho _ \pi变为(\mathcal Q'-Q)(p),这也就是\frac\gamma{1-\gamma}\mathcal Q'(\mathcal P-\mathcal P')\rho _ {\pi}。
先来看(\mathcal P-\mathcal P')\rho _ {\pi},可以对其1-范数进行估计:
\begin{aligned}
\|(\mathcal P-\mathcal P')\rho _ {\pi}\| _ 1&=\sum _ {s'}\Big|\sum _ s [P(s'|s)-P'(s'|s)]\rho _ \pi(s)\Big|\\
&\leqslant \sum _ {s,s'}|P(s'|s)-P'(s'|s)|\rho _ \pi(s)\\
&= \sum _ {s,s'}\Big|\sum _ a P(s'|s,a)[\pi(a|s)-\pi'(a|s)]\Big|\rho _ \pi(s)\\
&\leqslant \sum _ {s,s',a}P(s'|s,a)|\pi(a|s)-\pi'(a|s)|\rho _ \pi(s)\\
&= \sum _ {s,a}|\pi(a|s)-\pi'(a|s)|\rho _ \pi(s)\\
&= E _ {s\sim\rho _ \pi}\Big[\sum _ a|\pi(a|s)-\pi'(a|s)|\Big].
\end{aligned}Pinsker不等式(Pinsker不等式证明摘录)告诉我们,TV距离或者说1/2的L1距离小于等于\sqrt{\frac12D _ {\mathrm{KL}}},于是
\|(\mathcal P-\mathcal P')\rho _ {\pi}\| _ 1\leqslant \sqrt{2E _ {s\sim\rho _ \pi}[D _ {\mathrm {KL}}(\pi'\|\pi)(s)]}.
接下来看\rho _ {\pi'}-\rho _ \pi=\frac{\gamma}{1-\gamma}\mathcal Q'q,其中q=(\mathcal P-\mathcal P')\rho _ {\pi},有
\begin{aligned}
\|\rho _ {\pi'}-\rho _ \pi\| _ 1&=\frac{\gamma}{1-\gamma}\sum _ {s'}\Big|\sum _ s q(s)\sum _ k(1-\gamma)\gamma^k P'(s\stackrel{t=k}\to s')\Big|\\
&\leqslant \frac{\gamma}{1-\gamma}\sum _ {s}\sum _ {s',k}|q(s)|(1-\gamma)\gamma^kP'(s\stackrel{t=k}\to s')\\
&=\frac{\gamma}{1-\gamma}\|q\| _ 1\leqslant \frac{\gamma}{1-\gamma}\sqrt{2E _ {s\sim\rho _ \pi}[D _ {\mathrm {KL}}(\pi'\|\pi)(s)]}.
\end{aligned}这就证明了引理。我们继续看J(\pi')-J(\pi)=\frac1{1-\gamma}E _ {s\sim\rho _ {\pi'},a\sim\pi'}[A _ \pi(s,a)],用\rho _ {\pi}代替\rho _ {\pi'}的误差
\begin{aligned}
&\Big|J(\pi')-J(\pi)-\frac1{1-\gamma}E _ {s\sim\rho _ {\pi},a\sim\pi}\Big[\frac{\pi'(a|s)}{\pi(a|s)}A _ {\pi}(s,a)\Big]\Big|\\
={}&\frac{1}{1-\gamma}\Big|\sum _ s(\rho _ {\pi'}(s)-\rho _ \pi(s))E _ {a\sim\pi'}[A _ \pi(s,a)]\Big|\\
\leqslant{}&\frac{1}{1-\gamma}\sup _ s(E _ {a\sim\pi'}[A _ \pi(s,a)])\cdot\|\rho _ {\pi'}-\rho _ \pi\| _ 1\\
\leqslant{}&\frac{\sqrt2\gamma}{(1-\gamma)^2}\sup _ s(E _ {a\sim\pi'}[A _ \pi(s,a)]) \sqrt{E _ {s\sim\rho _ \pi}[D _ {\mathrm {KL}}(\pi'\|\pi)(s)]}.
\end{aligned}
令C(\pi')=\frac{\sqrt2\gamma}{(1-\gamma)^2}\sup _ s(E _ {a\sim\pi'}[A _ \pi(s,a)]),我们得到了如下的不等式:
命题(Relative policy performance bounds):
\begin{aligned}
&\Big|J(\pi')-J(\pi)-\frac1{1-\gamma}E _ {s\sim\rho _ {\pi},a\sim\pi}\Big[\frac{\pi'(a|s)}{\pi(a|s)}A _ {\pi}(s,a)\Big]\Big|\\
\leqslant{}&C(\pi')\sqrt{E _ {s\sim\rho _ \pi}[D _ {\mathrm {KL}}(\pi'\|\pi)(s)]}.
\end{aligned}同时,我们将s\sim\rho _ \pi变回原来的分布,
\frac1{1-\gamma}E _ {s\sim\rho _ {\pi},a\sim\pi}\Big[\frac{\pi'(a|s)}{\pi(a|s)}A _ {\pi}(s,a)\Big]=E _ \pi\Big[\sum _ {t=0}^\infty\gamma^t\frac{\pi'(a _ t|s _ t)}{\pi(a _ t|s _ t)}A _ {\pi}(s _ t,a _ t)\Big].就可以通过\pi生成的各episode来计算了。
Monotonic Improvement
我们原来的优化目标是\operatorname{\arg\max} _ {\pi'}(J(\pi')-J(\pi)),而从前面的命题可以得知
J(\pi')-J(\pi)\geqslant E _ \pi\Big[\sum _ {t=0}^\infty\gamma^t\frac{\pi'(a _ t|s _ t)}{\pi(a _ t|s _ t)}A _ {\pi}(s _ t,a _ t)\Big]-C(\pi')\sqrt{E _ {s\sim\rho _ \pi}[D _ {\mathrm {KL}}(\pi'\|\pi)(s)]}.假如我们对右边来进行优化,那么新policy优于原policy,这是因为当\pi'=\pi时,右边的值为0(注意到E _ \pi[A _ \pi(s _ t,a _ t)]=0),于是右边最大值非负,左边最大值自然也非负,就得到了一个提升过程。
现代诸多算法的做法是,用KL散度的“约束”来代替KL散度的“惩罚”。在优化领域,约束和惩罚之间替换是常见的做法。
考虑如下优化问题
\begin{aligned}
\pi _ {k+1}=\operatorname*{\arg\max} _ {\pi'}{}&E _ \pi\Big[\sum _ {t=0}^\infty\gamma^t\frac{\pi'(a _ t|s _ t)}{\pi(a _ t|s _ t)}A _ {\pi}(s _ t,a _ t)\Big],\\
\text{s.t. }&E _ {s\sim\rho _ {\pi _ k}}[D _ {\mathrm {KL}}(\pi'\|\pi _ k)(s)]\leqslant\delta _ k.
\end{aligned}可以大致认为和原问题是一样的。从这个约束版的优化问题出发,催生出一系列算法,如TRPO (Trust Region Policy Optimization)以及下面将要提及的PPO。
PPO算法
OpenAI提出的PPO算法有两种变体:Adaptive KL Penalty和Clipped Objective。原文可见:
Schulman, John, et al. "Proximal policy optimization algorithms." arXiv preprint arXiv:1707.06347 (2017).
Adaptive KL Penalty又回到了“惩罚”KL散度的优化问题,惩罚系数带“自适应性”。为简化记号新旧policy间的KL散度用D _ {\mathrm{KL}}(\boldsymbol\theta _ {k+1}\|\boldsymbol \theta _ k)记。
PPO w/ Adaptive KL Penalty 算法
初始化\boldsymbol\theta _ 0,\beta _ 0,\delta,然后执行以下循环
for k=1,2,\dots do
按policy \pi(\boldsymbol\theta _ k)收集每段长为T的分段数据
估计\hat A _ t\, (t=1,\dots,T)
计算policy的更新并按梯度下降更新若干次
\boldsymbol\theta _ {k+1}=\operatorname{\arg\max} _ {\boldsymbol\theta}\hat E _ {\pi _ k}[\sum\gamma^t\frac{\pi _ {\boldsymbol\theta}(a _ t|s _ t)}{\pi _ k(a _ t|s _ t)}\hat A _ t]-\beta _ k \hat D _ {\mathrm {KL}}(\boldsymbol\theta\|\boldsymbol\theta _ k)
if \hat D _ {\mathrm{KL}}(\boldsymbol \theta _ {k+1}\|\boldsymbol \theta _ k)\leqslant 1.5\delta
\beta _ {k+1}=2\beta _ k
else if \hat D _ {\mathrm {KL}}(\boldsymbol \theta _ {k+1}\|\boldsymbol \theta _ k)\geqslant \delta/1.5
\beta _ {k+1}=\beta _ k/2
end for
.
据称,这个算法比较稳健,\beta _ 0的初始选择影响很小,自适应性很强,里面的一些数如1.5,2都是较为随意地取的。多数迭代下KL散度都在所设范围内。
Clipped Objective的变体是OpenAI主要使用的版本。Clip函数的定义为\mathrm{clip}(x,a,b)=a\, \mathbb I(x<a)+x\, \mathbb I(a\leqslant x\leqslant b)+b\, \mathbb I(x>b),也就是把在[a,b]之外的都压到a或b。
PPO w/ Clipped Objective 算法
初始化\boldsymbol \theta _ 0,\epsilon
for k=1,2,\dots do
按policy \pi(\boldsymbol\theta _ k)收集每段长为T的分段数据
估计\hat A _ t\, (t=1,\dots,T)
计算policy的更新并按梯度下降更新若干次
\boldsymbol\theta _ {k+1}=\operatorname{\arg\max} _ {\boldsymbol\theta}L _ {\boldsymbol\theta _ k}^{\mathrm{CLIP}}(\boldsymbol\theta)
其中L _ {\boldsymbol\theta _ k}^{\mathrm{CLIP}}(\boldsymbol\theta)=\hat E _ {\pi _ k}[\min\{r _ t(\boldsymbol\theta)\hat A _ t,\mathrm{clip}(r _ t(\boldsymbol\theta),1-\epsilon,1+\epsilon)\hat A _ t\}]
end for
.
算法中的r _ t(\boldsymbol\theta)=\pi _ {\boldsymbol\theta}(a _ t|s _ t)/\pi(a _ t|s _ t)。为了和原算法保持一致,已经把求和项拆掉并忽略了discount因子(即已经让\gamma=1)。
来看其目标函数。当A是正数时,可以看出r<1+\epsilon时期望里的\min运算后都是rA,而r\geqslant 1+\epsilon时则是(1+\epsilon)A;当A<0,可以看出当r<1-\epsilon时\min运算后是(1-\epsilon)A,而r\geqslant 1-\epsilon时是rA。
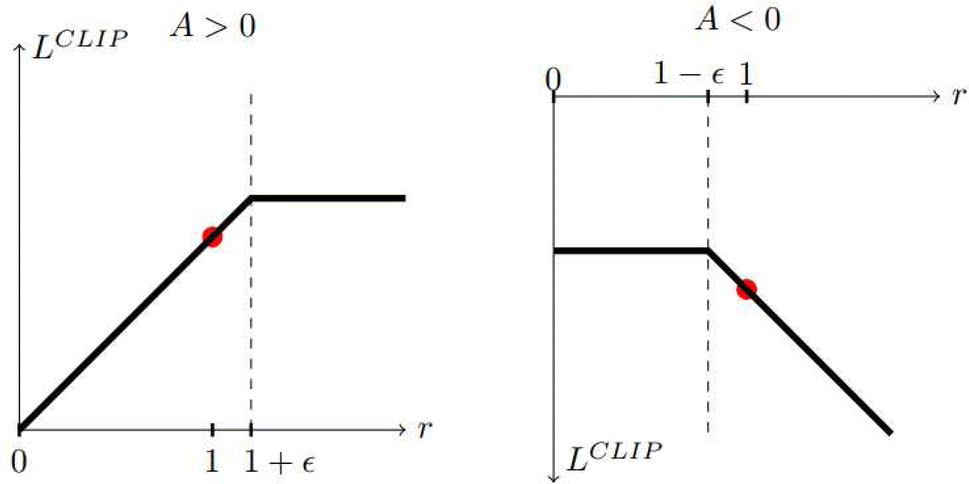
上图为PPO原文里的作图。
通过clip的方式,控制了新旧policy间的差异。
Generalized Advantage Estimator (GAE)
PPO算法中的估计advantage函数可以用GAE来做到。原文可见:
Schulman, John, et al. High-dimensional continuous control using generalized advantage estimation. arXiv preprint arXiv:1506.02438 (2015).
对于A函数的估计,可以是
\begin{aligned}
\hat A _ t^{(1)}&=r _ t+\gamma V(s _ {t+1})-V(s _ t),\\
\hat A _ t^{(2)}&=r _ t+\gamma r _ {t+1}+\gamma^2V(s _ {t+2})-V(s _ t),\\
&~\; \vdots\\
\hat A _ t^{(\infty)}&=r _ t+\gamma r _ {t+1}+\dots+\gamma^k r _ {t+k}+\dots-V(s _ t).
\end{aligned}现在引入一个定义:\delta _ t^V=r _ t+\gamma V(s _ {t+1})-V(s _ t),那么\hat A _ t^{(1)}=\delta _ t^V,\hat A _ t^{(2)}=r _ t+\gamma (r _ {t+1}+\gamma V(s _ {t+2}))-V(s _ t)=\delta _ t^V+\gamma \delta _ {t+1}^V,类似地可推知\hat A _ t^{(k)}=\sum _ {i=0}^{k-1}\gamma^i\delta _ {t+i}^V。
GAE里,引入了新的参数\lambda,然后考虑指数权重的估计
\begin{aligned}
\hat A _ t^{\mathrm{GAE}(\gamma,\lambda)}&=(1-\lambda)(\hat A _ t^{(1)}+\lambda\hat A _ t^{(2)}+\lambda^2\hat A _ t^{(3)}+\cdots)=(1-\lambda)\sum _ {k=0}^\infty\lambda^k\hat A _ t^{(k+1)}\\
&=(1-\lambda)\sum _ {k=0}^\infty\sum _ {i=0}^{k}\lambda^k\gamma^i\delta _ {t+i}^V=(1-\lambda)\sum _ {i=0}^\infty\sum _ {k=i}^{\infty}\lambda^k\gamma^i\delta _ {t+i}^V\\
&=\sum _ {i=0}^\infty(\gamma\lambda)^i\delta _ {t+i}^V.
\end{aligned}其中我们已假设能够交换求和号顺序(例如需要\lambda<1)。通过选择恰当的\lambda来做到bias-variance tradeoff。
PPO使用的便是truncated版本的GAE,写出来是
\hat A _ t=\delta _ t+(\gamma\lambda)\delta _ {t+1}+\dots+(\gamma\lambda)^{T-t-1}\delta _ {T-1}.当\lambda=1时,恰为A3C所使用的\hat A。
模仿学习
在本文开头,提到了一个很基本的假设:我们总能把要优化的目标建模成一个标量reward。很多时候这是很难做到的,或者能够建模但只是近似建模,这种近似可能会导致未知的不可控偏差。这种情况下,如果有一些能够模仿的demonstration样例,或许对其进行模仿更为容易。
现在我们考虑的是如下设置:
- \mathcal S,\mathcal A不变;
- 无reward函数;
- 一些demonstrations (s _ 0,a _ 0,s _ 1,a _ 1,\dots,),代表了要模仿的policy \pi^\ast。
下面从behavior cloning和Inverse RL两方面来看如何进行模仿学习。
Behavior cloning
Behavior cloning把问题化归到了标准的监督学习。以(s _ i,a _ i)作为一个数据,用s _ i预测a _ i,这就是训练一个policy \pi _ \theta(s)使得\|\pi _ {\theta}(s)-a\|^2最小,那么就是优化
\operatorname*{\arg\min} _ \theta E[\|\pi _ {\theta}(s)-a\|^2].也可以把(s _ 0,a _ 0,s _ 1,a _ 1,\dots)看作是序列数据,BC-RNN就是使用RNN作为policy的建模。
虽然这种BC简单明了,一个明显的问题是训练和测试分布不一致。训练时的label分布由\pi^\ast确定:s _ {t+1}\sim P(\cdot|s _ t,\pi^\ast(s _ t)),但测试时分布却由\hat\pi(s)确定。这种不一致会轻易导致训练得很好的模型测试表现很差——\hat\pi(s)可以让agent见到大量陌生的state。
一种弥补方案就是让expert持续指导agent。
DAGGER: Dataset Aggregation
初始化\pi _ 1,\mathcal D\leftarrow\varnothing
for i=1 to N do
令\pi _ i=\beta _ i\pi^\ast+(1-\beta _ i)\hat\pi _ i
以policy \pi _ i行动得到一列s
令\mathcal D _ i=\{(s,\pi^\ast(s))\},\mathcal D\leftarrow \mathcal D\bigcup\mathcal D _ i
在\mathcal D上训练\hat\pi _ {i+1}
end for
这个算法的关键缺陷正是在于需要expert持续性指导。
Inverse Reinforcement Learning (IRL)
IRL考虑的则是将reward先恢复出来,再学习policy。
在原RL里,我们要找policy使得R之下的return最大,而在IRL里,则是找R使得demonstration下的policy是最优policy。许多方法都可以做到这一点,影响力比较大的是Maximumum Entropy Inverse Reinforcement Learning和Generative adversarial imitation learning。这里只看后者(虽然准确来说不严格算IRL)。
- ZIEBART, Brian D., et al. Maximum entropy inverse reinforcement learning. In: AAAI. 2008. p. 1433-1438.
- HO, Jonathan; ERMON, Stefano. Generative adversarial imitation learning. Advances in neural information processing systems, 2016, 29.
GAN已在 link 有过回顾。在GAN里,生成器网络直接生成样本\boldsymbol{x}=g(\boldsymbol{z}),使得\boldsymbol{x}的分布和p _ {\mathrm{data}}越接近越好,让判别器难以区分。这种对抗性和模仿学习里有类似之处,我们也可以设置一个判别器判别agent生成的数据和expert的数据。这里agent就扮演了生成器的角色。
Generative adversarial imitation learning (GAIL)算法:
初始化略
for i=0,1,\dots do
采样agent的trajectory \tau _ i\sim\pi _ {\boldsymbol\theta _ i}
更新判别器参数\boldsymbol{w} _ i至\boldsymbol{w} _ {i+1},更新梯度为:
\hat E _ {\tau _ i}[\nabla _ {\boldsymbol{w}}\ln D _ {\boldsymbol{w}}(s,a)]+\hat E _ {\tau^\ast}[\nabla _ {\boldsymbol{w}}\ln(1-D _ {\boldsymbol{w}}(s,a))]
更新policy参数\boldsymbol{\theta} _ i至\boldsymbol{\theta} _ {i+1},优化目标为:\ln (D _ {\boldsymbol{w} _ {i+1}}(s,a))
RL from human feedback (RLHF)
本节我们继续考虑没有reward的情况。对这种情况,一种想法是通过比较来反映人的偏好。不难想象,“比较”是比“赋分”更为容易的。如果我们建立的reward模型的排序结果,和任选一对间的比较结果是一致的,那么这个reward模型应该合理。
Bradley–Terry模型
在Bradley–Terry模型里,设i,j的指数赋分分别为\mathrm e^{\beta _ i},\mathrm e^{\beta _ j},它们反映了i,j对外比较时的“优势大小”——i优于j的概率为
P(i\succ j)=\frac{\mathrm e^{\beta _ i}}{\mathrm e^{\beta _ i}+\mathrm e^{\beta _ j}}=\frac{1}{1+\exp(-(\beta _ i-\beta _ j))}.这就联系起了Logistic模型。
记reward模型为R _ \phi,我们得到一系列比较数据\{(x _ w,x _ l)\},其中x _ w为比较中更优的数据,x _ l则是比较中不如x _ w。那么训练的损失就为
L _ R(\phi)=-E[\ln\sigma(R _ \phi(x _ w)-R _ \phi(x _ l))].
在NLP自然语言处理的语境下,我们用x记instruction,y记output,当我们有一个预训练LM p _ \theta(y|x)和一个待训练的reward函数R _ {\phi}(x,y),reward函数的损失现为
L _ R(\phi)=-E _ {x,y _ w,y _ l\sim\mathcal D}[\ln\sigma(R _ \phi(x,y _ w)-R _ \phi(x,y _ l))].
训练好reward模型后,RLHF即优化-E _ {\hat y\sim p _ \theta(\hat y|x)}[R _ \phi(x,\hat y)],但为了减小reward函数的不良影响,加上一个KL散度的惩罚项:
L(\boldsymbol\theta)=-E _ {\hat y\sim p _ {\boldsymbol\theta}(\hat y|x)}\Big[R _ \phi(x,\hat y)-\beta\ln \frac{p _ {\boldsymbol\theta}(\hat y|x)}{p _ 0(\hat y|x)}\Big].
Direct preference optimization (DPO)
非常现代的一个简明算法。
RAFAILOV, Rafael, et al. Direct preference optimization: Your language model is secretly a reward model. Advances in Neural Information Processing Systems, 2024, 36.
下面继续考虑上面的NLP语境(即沿用上面记号)。我们首先直接求解RLHF的损失函数的优化,期望里的项可重写为
\begin{aligned}
&-\beta\Big(-\frac1\beta R _ \phi(x,\hat y)+\ln\frac{p _ {\boldsymbol\theta}(\hat y|x)}{p _ 0(\hat y|x)}\Big)=-\beta\ln\frac{p _ {\boldsymbol\theta}(\hat y|x)}{p _ 0(\hat y|x)(\exp\frac1\beta R _ \phi(x,\hat y))}\\
={}&-\beta\ln\frac{p _ {\boldsymbol\theta}(\hat y|x)}{p _ 0(\hat y|x)(\exp\frac1\beta R _ \phi(x,\hat y))\mathbin{/} Z(x) }+\beta\ln Z(x),
\end{aligned}这里Z(x)=\sum _ yp _ 0(\hat y|x)(\exp\frac1\beta R _ \phi(x,\hat y)),这样上式分母成为一个分布,记为p^\ast(\hat y|x),那么
\operatorname*{\arg\min} _ {\boldsymbol{\theta}}L(\boldsymbol{\theta})=\operatorname*{\arg\min} _ {\boldsymbol{\theta}} E _ {\hat y\sim p _ {\boldsymbol{\theta}}(\hat y|x)}\Big[\ln\frac{p _ {\boldsymbol\theta}(\hat y|x)}{p^\ast(\hat y|x)}\Big]=\operatorname*{\arg\min} _ {\boldsymbol{\theta}}D _ {\mathrm{KL}}(p _ {\boldsymbol{\theta}}\|p^\ast).显然p _ {\boldsymbol{\theta}}=p^\ast时L最小。我们也可以用p^\ast反过来表示R _ \phi:
\begin{aligned}
&p^\ast(\hat y|x)=p _ 0(\hat y|x)(\exp\tfrac1\beta R _ \phi(x,\hat y))\mathbin{/}Z(x)\\
\implies{}&R _ \phi(x,\hat y)=\beta\ln\frac{p^\ast(\hat y|x)}{p _ 0(\hat y|x)}+\beta\ln Z(x).
\end{aligned} p^\ast和R _ \phi之间有一一对应关系。
现在再回到R _ \phi的训练,回顾reward函数的损失,L _ R(\phi)=-E _ {x,y _ w,y _ l\sim\mathcal D}[\ln\sigma(R _ \phi(x,y _ w)-R _ \phi(x,y _ l))],
可以看到Bradley–Terry模型里起作用的是R _ \phi的差,上述表示就带来了一些便利:
L _ {\mathrm{DPO}}(\boldsymbol\theta)=-E _ {x,y _ w,y _ l\sim\mathcal D}\Big[\ln\sigma\Big(\beta\ln\frac{p _ {\boldsymbol{\theta}}(y _ w|x)}{p _ 0(y _ w|x)}-\beta\ln\frac{p _ {\boldsymbol{\theta}}(y _ l|x)}{p _ 0(y _ l|x)}\Big)\Big].
于是,我们可以直接对上式进行优化,reward模型变为了隐式地训练。
DPO简单明了、计算方便,现已十分流行,众多开源LLM都在使用。
离线(Offline)强化学习
在前面的设置中,agent是通过不断地与环境交互得到反馈,从中学习从而变得更为“智能”。这并不总是方便的,很多时候与环境交互需要高昂的成本或风险,这时候仅从已有的静态数据、不与环境交互来学习一个比较好的policy,成为了一个非常值得研究的问题。这也将问题变得与熟悉的ML里的监督学习更为相像。如今正是大数据时代,从海量数据中挖掘有价值的信息是极为有必要甚至是迫切的,因而这种学习模式前景广阔。这种模式一般称作是离线强化学习(offline RL),或是batch RL。
离线RL在近些年受到越来越多的关注,但现在只能说仍是underexplored,因而这里也只是走马观花,仅是极为粗略的叙述。更多可以参见:
PRUDENCIO, Rafael Figueiredo; MAXIMO, Marcos ROA; COLOMBINI, Esther Luna. A survey on offline reinforcement learning: Taxonomy, review, and open problems. IEEE Transactions on Neural Networks and Learning Systems, 2023.
在Q-learning中,每次迭代我们对Q函数的更新为Q(s _ t,a _ t)\leftarrow Q(s _ t,a _ t)+\alpha[r _ t+\gamma\max _ a Q(s _ {t+1},a)-Q(s _ t,a _ t)],那么收敛时应有r(s _ t,a _ t)+\gamma\max _ aQ(s _ {t+1},a)\approx Q(s _ t,a _ t)。如果在离线设置下我们也用这个方式学习一个Q函数,那么[r(s,a)+\gamma\max _ {a'}Q(s',a')- Q(s,a)]^2可以预期也会很小,但由于训练是在数据集\mathcal D=\{(s,a,r,s')\}是进行的,这个“小”应是相对于\mathcal D来说的,就是说训练最终使得E _ {\pi _ \beta}[r(s,a)+\gamma\max _ {a'}Q(s',a')- Q(s,a)]^2小(这里\pi _ \beta代表的是\mathcal D的数据源的分布\pi _ \beta(a|s),一般称behavior policy)。然而我们真正希望的是在\hat\pi=\operatorname{\arg\max} _ aQ(s,a)下的E _ {\hat\pi}[r(s,a)+\gamma\max _ {a'}Q(s',a')- Q(s,a)]^2足够小,这样才能让Q-learning“生效”。因而,一般直接在离线设置下进行这种类Q-learning时,效果都会不够理想。
一种经典的Offline RL的思路是policy constraint。对\mathcal D中少见的数据,对应的Q函数估计效果会不好,那么agent就有可能据此选择我们并不期望的action。因而可以考虑学习一个和behavior policy \pi _ \beta相近的\pi _ {\boldsymbol\theta},比如说,我们加上一个约束D _ {\mathrm {KL}}(\pi _ {\boldsymbol{\theta}}\|\hat\pi _ \beta)\leqslant\epsilon。BCQ (batch constrained Q-learning)是另一个例子,考虑的是\pi _ {\boldsymbol{\theta}}=\operatorname{\arg\max} _ {a _ i+\xi _ {\boldsymbol{\theta}}(s,a _ i)}\{Q(s,a _ i+\xi _ {\boldsymbol{\theta}}(s,a _ i))\mid a _ i\sim\hat \pi _ \beta(\cdot|s),\, i=1,\dots,N\},估计的\hat\pi _ \beta是用一个生成模型来做到,能生成与\mathcal D相近的N个action用于Q函数的训练,而\xi _ {\boldsymbol{\theta}}(s,a)则是一个微扰,用于增加生成action的多样性。不难看出,当N=1、微扰置为零时,BCQ相当于限制\pi _ {\boldsymbol\theta}=\pi _ \beta,而当N\to\infty、微扰不设限时,就是前一段所说的“类”Q-learning了。
除了显式的约束,隐式的约束,从而规避对\pi _ \beta的估计,也是可行的。由于是带约束的优化,我们可以考虑KKT条件,然后解出\pi^\ast的闭式解,再找出和它最接近的\pi _ {\boldsymbol{\theta}}。于是可以导出优化问题J(\boldsymbol{\theta})=E _ {\mathcal D}[\ln\pi _ {\boldsymbol{\theta}}(a|s)\exp(\frac1\lambda\hat A _ \pi(s,a))],得到\pi _ {\mathrm{new}}(a|s)。这里的policy improvement涉及的训练只需要\pi _ \beta的数据而无需显式估计\pi _ \beta,就施加了D _ {\mathrm{KL}}\leqslant\epsilon的约束。进一步,在policy evaluation里,也可以试图做到。在IQL(implicit Q-learning)里,引入了一个新网络V^{\boldsymbol{\psi}},Q函数的更新是相对于J(\boldsymbol\phi)=E _ {\mathcal D}[r(s,a)+\gamma V^{\boldsymbol{\psi}}(s')-Q^{\boldsymbol{\phi}}(s,a)],而V函数则是选择恰当的l(\cdot)使得优化E _ {\mathcal D}[l(V^{\boldsymbol{\psi}}(s)-Q^{\boldsymbol{\phi}}(s,a))]收敛到合适的地方。收敛到这里就可以说是“合适的”:V(s)=\max _ {a\in\Omega(s)}Q(s,a),\Omega(s)=\{a\mid \pi _ \beta(a|s)\geqslant \epsilon\},相当于数据集能支持的“最优解”。以上就是IQL的思路。
最后简要看下CQL (Conservative Q-learning)的思路。CQL在常规目标函数上添加了一项正则项用以降低过大的Q函数值,因为对于\mathcal D中罕见的action,我们自然会想要保守估计Q。考虑先添加正则项\max _ \mu E _ {s\sim \mathcal{D},a\sim\mu(a|s)}[Q(s,a)]。可以证明当正则项的系数满足一定条件时,训练出的Q函数确实是真实Q函数的保守估计:\hat Q _ \pi\leqslant Q _ \pi。但对于\mathcal D中的高频action,或许不需要太多保守估计,因而正则项现写为\max _ \mu E _ {s\sim \mathcal{D},a\sim\mu(a|s)}[Q(s,a)]-E _ {(s,a)\sim\mathcal D}[Q(s,a)],这样对于\mathcal D中的数据,第二项会抵消第一项对Q的降低效应。此时,在期望意义上Q函数是保守估计:E _ {\pi(a|s)}[\hat Q(s,a)]\leqslant E _ {\pi(a|s)}[Q(s,a)]。CQL还加入了对\mu的正则项,现在正则项为
\max _ \mu E _ {s\sim \mathcal{D},a\sim\mu(a|s)}[Q(s,a)]-E _ {(s,a)\sim\mathcal D}[Q(s,a)]-\mathcal R(\mu).常见的选择是\mathcal R(\mu)=E _ {s\sim\mathcal D}[\mathcal H(\mu)],这样正则项里的\mu有闭式解,方便计算或者估计。
Offline RL还有model-based的方法,等等。此处不作叙述了。
MCTS与AlphaGo
MCTS全称Monte Carlo Tree Search,按名称可看出是一种树搜索算法。其最著名的成就或许就是让AlphaGo在围棋上击败人类顶尖棋手了。本节先来看MCTS的步骤,再看它在AlphaGo上的应用。
Monte Carlo Tree Search
在步骤上,MCTS每一次循环有四步。每到一次新state,可以执行MCTS来选择当下应选的action,然后在新的state再执行新的MCTS。
- Selection:从树的根节点出发(即为当前state),通过一个tree policy,逐步到达树的一个叶节点。
- Expansion:某些迭代中,树会在所选的叶节点之下增加(未探索的action的)节点。
- Simulation:在新节点之下进行完整episode的模拟,一次模拟可称作一rollout;在树之外的action采取的是简单易行的rollout policy。
- Backup(back-propagation):根据模拟结果,更新统计数据。
Tree policy会倾向于选择更优的节点,例如以\epsilon-greedy作为tree policy时就是如此。因而在循环达到一定次数后,被选择最多的那个action应该就是最好的,于是在最后agent实际选择的action就是这个action。到了新的state,旧的树的无关部分就全部舍弃了,相关部分则继续沿用。
AlphaGo
AlphaGo引入了两个神经网络——value网络v _ {\boldsymbol{\theta}}和policy网络p _ {\boldsymbol{\sigma}}。Value网络提供了一个模拟之外的评估节点的方式,policy网络则是应用在expansion阶段,预测哪个action来展开树是最好的。Policy网络架构上是13层的CNN,通过在人类棋手上的数据以监督学习(supervised learning)训练得到,我们称SL policy网络。训练后的SL policy网络将能够预测人类顶尖棋手在面对各种state会下出的最可能的下法。而对于value网络,除了输出层是输出一个标量结构和SL policy网络是一样的。其训练分两步:首先用强化学习训练再一个初始化在SL policy网络的policy网络p _ {\boldsymbol{\rho}},我们称RL policy网络。通过前面policy gradient的理论,可知\boldsymbol\rho的更新可为
\Delta\boldsymbol{\rho}\propto\frac{\partial\ln p _ {\boldsymbol{\rho}}(a _ t|s _ t)}{\partial\boldsymbol{\rho}}z _ t,其中z _ t按胜负取+1,-1。第二步则是通过p _ {\boldsymbol{\rho}}间的自我对弈来训练value网络,这是一个回归的训练,最小化MSE。
Rollout policy也是通过人类数据上的监督学习完成,但由于需要其简单易行,就只是采用了一个线性网络。
在MCTS的selection阶段,tree policy为
a _ t=\operatorname*{\arg\max} _ a \Big[Q(s _ t,a)+c\frac{\pi(a|s _ t)\sqrt{N(s _ t)}}{1+N(s _ t,a)}\Big].其中的\pi(a|s)由SL policy网络p _ {\boldsymbol{\sigma}}提供。第一项照顾了exploitation,第二项照顾了exploration。
Expansion阶段,用SL policy网络完成。
Simulation阶段,对叶节点的评估为
v(s)=(1-\eta)v _ {\boldsymbol{\theta}}(s)+\eta G,其中G是rollout的return。
Backup阶段,照常,更新N(s,a),Q(s,a)。
AlphaGo Zero
与前面的AlphaGo相比,它们有一些非常重要的不同:首先,Zero是纯强化学习得到的,不再用到监督学习,AlphaGo里用到了一些人类棋手数据做监督学习。其次,特征学习方面,Zero的网络仅用到了最原始的特征,原Go里则用到了一些手工设计的特征。再次,Zero仅需要一个网络,原Go需要value网络和policy网络两个网络。最后,Zero不再通过rollout模拟来进行评估,原Go里rollout的结果占评估的一半比重。
Zero利用的关键一点是:对于一个policy,如果进行MCTS时用它来做selection步,那么最后在根节点得到的是比原policy更优的policy。就是说,MCTS可以看作是一种policy improvement operator。
Zero在自我对弈时,每一步进行MCTS会进行1600次循环,来选出当下的下法。每一次循环,selection仍是按使Q(s _ t,a)+c\frac{P(s _ t,a)\sqrt{N(s _ t)}}{1+N(s _ t,a)}最大的a来选择,到达叶节点后就是expansion,得到的s用神经网络评估:f _ {\boldsymbol{\theta}}(s)=(P(s,\cdot),V(s)),最后backup进行相应的更新。循环结束后,按N^{1/\tau}的比例返回概率\boldsymbol{\pi},其中N代表总访问次数,\tau是一个“温度”参数。这个过程,如果把MCTS记作\alpha,可以表示为\boldsymbol{\pi} _ t=\alpha(s _ t;\boldsymbol{\theta} _ {i-1})。
一局自我对弈在T步完成后,我们有T个(s _ t,\boldsymbol{\pi} _ t,z _ t),其中z _ t=r _ T=\pm1代表对弈结果。从这些数据,可以将参数\boldsymbol{\theta} _ {i-1}更新到\boldsymbol{\theta} _ {i},学习目标是让f _ {\boldsymbol{\theta}}(s)=(\boldsymbol{p},V)更接近(\boldsymbol{\pi},z)。
AlphaGo Zero在原AlphaGo上更上一层楼,当下人类顶尖棋手不能望其项背,充分展现出人工智能的强大。

发表回复